Extension quadratique de Q
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 20:02
par barbu23 » 20 Nov 2009, 20:02
Bonsoir à tous : :happy3:
Soit

un entier relatif sans facteur carré ( que signifie : sans facteur carré ? :hein: ).
Pourquoi
 $)
est une extension de degré

de
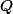
?
Merci de votre aide ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 20:05
par barbu23 » 20 Nov 2009, 20:05
J'ai pensé définir une application de la forme suivante :
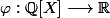
telle que :
 = P(\sqrt{d}) $)
Mais après, je ne sais pas quoi faire ! Je ne sais pas si c'est correct ce que j'écris ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 20:27
par barbu23 » 20 Nov 2009, 20:27
Help plz ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 20:29
par barbu23 » 20 Nov 2009, 20:29
Ben314, tu peux me donner un coup de main à cet exo ? Merci ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Nov 2009, 20:45
par Ben314 » 20 Nov 2009, 20:45
Sans facteur carré signifie qu'il n'est divisible par aucun carré entier distinct de 1 (i.e. que dans sa décomposition en nombre premier, tout les nombres premiers sont distincts)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Nov 2009, 20:55
par Ben314 » 20 Nov 2009, 20:55
Le "degrés" d'une extention est la dimension de l'extention vue comme espace vectoriel sur le corps de départ.
Soit tu as vu que K[X]/P où P est un polynôme IRREDUCTIBLE sur K est une extention de K de degrés le degrés du polynôme P et dans ce cas il suffit d'expliquer pourquoi X^2-d est irréductible sur Q (c'est là qu'intervient le "sans facteur carré")
Soit tu ne l'as pas vu et il faut "à la main" montrer que les classes de 1 et de X dans le quotient forment une base du quotient...
Je suis en train de réfléchir que, temps que l'on n'as pas vu le résultat ci dessus, il n'est pas clair que K[X]/P soit un corps (ce n'en est un que si P est irréductible)
Fait attention à ton "idée" car rien dans l'énoncé ne précise que d est positif. s'il est négatif, ta fonction n'est pas la bonne (en plus je ne suis pas sure qu'elle serve à quelque chose pour calculer le degrés de l'extention)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 21:58
par barbu23 » 20 Nov 2009, 21:58
Et pourquoi :
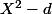
est irréductible ? :hein: :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Nov 2009, 22:04
par barbu23 » 20 Nov 2009, 22:04
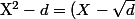(X+\sqrt{d}) $)
:hein: ( n'est pas irréductible ? ) :hein:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Nov 2009, 23:33
par Ben314 » 20 Nov 2009, 23:33
Tu as parfaitement raison, le fait que
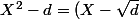(X+\sqrt{d}))
montre que
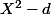
n'est irréductible dans aucun corps contenant une racine de

.
Par exemple
1) sur
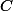
le polynome n'est jamais irréductible (quelque soit la valeur de

)
2) sur

le polynome n'est jamais irréductible si
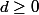
par contre il est irréductible si
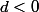
3) sur
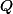
, si
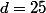
le polynôme n'est pas irréductible...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités