Extension de corps
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 11 Juin 2017, 17:05
par chombier » 11 Juin 2017, 17:05
Bonjour,
Je planche désormais sur cette fiche :
https://d396qusza40orc.cloudfront.net/i ... os/Ex2.pdfJ'essaie de faire l'exercice 2, j'ai avancé un peu mais je marche sur des oeufs, je joue un peu à l'apprenti sorcier, j'aimerais donc bien être relu et puis... je suis vite coincé :
D'abord, on remarque que

, donc

.
)
est une base de

dans

Considéront alors
)
. C'est un sous-espace vectoriel de L(V) isomorphe à

Je ne sais même pas si ce que je dis a vraiment du sens


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 12 Juin 2017, 08:27
par zygomatique » 12 Juin 2017, 08:27
salut

est un corps contenant
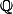
donc V est naturellement muni d'une structure d'espace vectoriel sur ce corps :
pour tout vecteur u et v de V et tout scalaire x et y de K xu + yv appartient à V
peut-être faut-il être plus précis sur la multiplication externe ... et vérifier qu'on a toujours f(xu + yv) = xf(u) + yf(v) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Juin 2017, 07:56
par zygomatique » 13 Juin 2017, 07:56
pour tout x et y dans Q et u et v dans V alors xu + yv est dans V
or
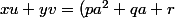 u + (p'a^2 + q'a + r')v)
pour des rationnels p, q, r, p', q' et r'
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 14 Juin 2017, 11:30
par Archytas » 14 Juin 2017, 11:30
zygomatique a écrit:
est un corps contenant
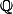
donc V est naturellement muni d'une structure d'espace vectoriel sur ce corps
C'est un peu ambitieux, non ?
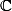
est un corps contenant

pourtant on aura du mal à munir
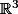
ou même

d'une structure de
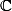
-espace vectoriel.
Selon moi le plus naturel serait de redéfinir directement le produit externe:
.v :=a.v+b.f(v)+c.f^2(v))
Puis vérifier qu'avec cette définition on a bien un

-espace vectoriel.
Je me trompe peut être je n'ai pas vérifié tous les axiomes mais intuitivement ça m'a l'air bien huilé.
Pour la dimension, on pourrait s'inspirer de la fameuse formule


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Juin 2017, 12:20
par zygomatique » 14 Juin 2017, 12:20
tu as surement raison et je me demandais d'ailleurs comment utiliser f ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 14 Juin 2017, 12:23
par Archytas » 14 Juin 2017, 12:23
Tu as dû t’emmêler les pinceaux, ce qui est vrai c'est si K est une extension de k et V est un K-espace vectoriel alors V peut être muni d'une structure de k-espace vectoriel, mais le contraire ne marche pas toujours (ici heureusement ça marche ^^)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités

