Exo sur la connexité

[Epsilon]

bonjour
voila je cherche la solution de cet exo

Merci d'avance

[fahr451]

bonjour
1)
supposons X conn et soit f continue
{0} et {1} sont ouverts
les images réciproques sont ouvertes et recouvrent X donc l'une est vide et f constante

supposons qu 'il existe f continue non c onstante alors de même X est partitionné en deux ouverts non vides disjoints ce qui assure que X non connexe

[legeniedesalpages]

Bonjour,

Juste une question fahr451,

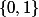
Quand on parle de l'espace , quelle topologie est définie implicitement? la discrète? la topo induite de la droite ?
Ou encore une autre?

[fahr451]

bonjour

discrète et induite c'est la même ici
{0} est la trace de l'ouvert]-1/2 ,1/2[

[legeniedesalpages]

oui c'est vrai :mur:

[legeniedesalpages]

pour la 3) l'idée je pense que c'est qu'on considère deux points de .

Donc il existe tels que et . On peut supposer sans perdre de généralité que .

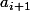
Pour tout , il existe , et par la connexité de chacun de ces , on peut relier par un chemin et , et pour tout i, et et.

Je pense qu'il faut creuser dans ce sens.

[fahr451]

attention connexe par arcs et connexe ne sont pas deux notions identiques
j'attends une réaction à ma réponse du 1) pour éventuellement poursuivre mon aide

[quinto]

Je pense qu'il faut creuser dans ce sens.

Non,
ici tu utilises la connexité par arcs, mais rien ne nous dit que nos ensembles sont connexes par arcs, on sait juste qu'ils sont connexes ...

[legeniedesalpages]

ah oui désolé, je croyais que c'était la définition de la connexité, effectivement j'ai confondu avec la définition de la connexité par arcs.

Edit: bon en fait, je galère à voir pour la 2) et la 3) je vais chercher en attendant une réaction d'epsilon au lieu de raconter n'importe quoi :)

[legeniedesalpages]

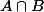
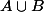
pour la 3) si je montre que si A et B sont deux parties connexes et que est non vide, alors est connexe.

Par récurrence, je peux généraliser ce résultat par une récurrence et l'associativité de l'intersection à une union finie de connexes "deux à deux liés", mais je ne vois pas comment généraliser ce résultat à une union dénombrable?

[fahr451]

pour le 3

prendre U1 et U2 deux ouverts disjoints qui recouvrent l 'union des An

on peut supposer que A0 rencontre U1 on a ensuite que A0 est inclus dans U1 puis A2 rencontre U1 puis A2 inclus dans U1 etc l'union est incluse dans U1

[legeniedesalpages]

ah oui c'est vrai donc U2 est vide et l'union est connexe.
ok merci fahr451. :we:

[fahr451]

donc U2 inter U An est vide plutôt

une correction: tout dépend ce que tu as supposé sur U1 et U2 au départ

pour moi recouvrent c 'est UAn inclus dans U1 U U2
U1 et U2 ouverts de E


mais si tu supposes UAn = U1 U U2 avec u1 et U2 ouverts de UAn

tu arrives en effet à U2 vide

[legeniedesalpages]

ah oui pardon :marteau: