Salut à tous,
je me pose une petite question... Pour montrer qu'un ensemble était connexe par arc en colle j'ai montré qu'il était convexe dans R donc connexe dans R, et j'en ai déduit connexe par arc en pensant que c'était la même chose. Il semble que notre prof ait mélangé allégrement dans le cours connexe et connexe par arc, et qui n'a pas plu au colleur ^^ Quelle est la différence ?
Merci d'avance
Connexité Versus Connexité par arc
10 messages
- Page 1 sur 1
Bonsoir,
j'ai mon bouquin qui donne un exemple d'espace connexe mais pas par arc, mais ça doit être dur à montrer:
On prend le graphe de l'application
de l'application ) de
de 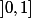 dans
dans  , c'est une image continue de
, c'est une image continue de 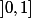 , donc c'est une partie connexe de
, donc c'est une partie connexe de  , sa fermeture
, sa fermeture  , qui est la réunion de
, qui est la réunion de  et de l'intervalle
et de l'intervalle  est aussi connexe. Mais
est aussi connexe. Mais  n'est apparemment pas connexe par arcs.
n'est apparemment pas connexe par arcs.
Après je ne saurai pas te dire pourquoi.
Donc dans , la notion de connexité et de connexité par arcs seraient différentes.
, la notion de connexité et de connexité par arcs seraient différentes.
En espérant que ça t'aide.
j'ai mon bouquin qui donne un exemple d'espace connexe mais pas par arc, mais ça doit être dur à montrer:
On prend le graphe
Après je ne saurai pas te dire pourquoi.
Donc dans
En espérant que ça t'aide.
connexe = qui ne peut pas s'écrire comme réunion de deux ouverts disjoints non vides. (on peut mettre fermé à la place d'ouvert).
Connexe par arc = tel que deux points quelconques sont reliés par un arc continu et inclus dans l'ensemble.
L'exemple de géniedesalpages est pas dur à traiter. On peut pas relier le point O à un point de la courbe.
Autre exemple : Soit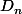 la droite d'équation
la droite d'équation 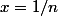 et
et  le segment
le segment ,1/n]\times \{n\}) . La réunion des
. La réunion des 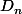 , des
, des  et de l'axe des ordonnées donne une partie connexe et pas connexe par arcs.
et de l'axe des ordonnées donne une partie connexe et pas connexe par arcs.
Connexe par arc = tel que deux points quelconques sont reliés par un arc continu et inclus dans l'ensemble.
L'exemple de géniedesalpages est pas dur à traiter. On peut pas relier le point O à un point de la courbe.
Autre exemple : Soit
bjr,
concernant la courbe de la fonction
) pour
pour 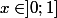
Son graphe est connexe car c'est l'image dans R^2 de l'intervalle
(connexe) ]0;1] par la fonction))
l'adhérence de son graphe est connexe (thm de topologie générale: l'adhérence d'une partie connexe est connexe). Pour obtenir l'adhérence du graphe,
on rajoute le segment de l'axe y'oy : [-1;1].
Si l'adhérence était connexe par arc, un arc joignant un point du graphe
à un point de l'axe y'oy serait rectifiable.
Or la longueur d'arc correspondante serait de même nature que
l'intégrale
})
qui est une intégrale divergente.
En gros, les arcs joignant un point du graphe à un point de l'adhérence, sur l'axe y'oy sont de longueur infinie.
Un argument qui n'utilise pas la différentiabilité:
La fonction)
ne vérifie pas le critère de Cauchy à droite de zéro:
-f(x')|< \epsilon)
ce qui interdit un arc continu joignant un point de la courbe
à un point de l'adhérence sur l'axe y'oy.
concernant la courbe de la fonction
Son graphe est connexe car c'est l'image dans R^2 de l'intervalle
(connexe) ]0;1] par la fonction
l'adhérence de son graphe est connexe (thm de topologie générale: l'adhérence d'une partie connexe est connexe). Pour obtenir l'adhérence du graphe,
on rajoute le segment de l'axe y'oy : [-1;1].
Si l'adhérence était connexe par arc, un arc joignant un point du graphe
à un point de l'axe y'oy serait rectifiable.
Or la longueur d'arc correspondante serait de même nature que
l'intégrale
qui est une intégrale divergente.
En gros, les arcs joignant un point du graphe à un point de l'adhérence, sur l'axe y'oy sont de longueur infinie.
Un argument qui n'utilise pas la différentiabilité:
La fonction
ne vérifie pas le critère de Cauchy à droite de zéro:
ce qui interdit un arc continu joignant un point de la courbe
à un point de l'adhérence sur l'axe y'oy.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
