Exo dénombrement mur
18 messages
- Page 1 sur 1
Exo dénombrement mur
Bonjour,
J'ai un exercice de dénombrement que j'ai vraiment envie de trouver, mais il me semble que je vais avoir besoin d'un coup de pouce...
La question : Combien peut-on former de murs distincts avec n briques identiques ? Sachant que l'on construit les murs sans trou ni surplomb, et que les briques sont donc contenues dans un unique plan vertical, posées soit au sol, soit sur une autre brique.
(j'en appelle aux amateurs de Minecraft, mais, moi, ça me dépasse...)
Voilà mon angle d'attaque :
J'ai raisonné sur les différentes hauteurs des briques du mur, des briques situées sur la ligne plus basse jusqu'aux briques potentiellement situées sur la n-ième ligne (je dis potentiellement, car il n'est pas certain qu'il y en ait sur la n-ième ligne, c'est même le cas dans une unique configuration, et pour une brique, le cas où elles sont toutes les unes sur les autres)
On définit les n-listes (H1, H2,..., Hn) chaque Hi étant le nombre de briques présentes sur la i-ème ligne.
On doit avoir H1 + H2 + H3 + ... + Hn = n (puisqu'il y a n briques)
Et aussi H1 >= H2 >= ... >= Hn (car une rangée ne peut comporter plus de briques que celle du dessous, sinon problème)
Le nombre de n-listes ainsi définies donne la réponse au problème. Reste à les compter. Et là, c'est la stagnation totale.
On a déjà fait des exercices où il est question de compter des p-listes lorsque la somme de leurs p composantes est égale à un entier donné. Mais là, on leur rajoute en plus un ordre...
Bref, help me, please !
J'ai un exercice de dénombrement que j'ai vraiment envie de trouver, mais il me semble que je vais avoir besoin d'un coup de pouce...
La question : Combien peut-on former de murs distincts avec n briques identiques ? Sachant que l'on construit les murs sans trou ni surplomb, et que les briques sont donc contenues dans un unique plan vertical, posées soit au sol, soit sur une autre brique.
(j'en appelle aux amateurs de Minecraft, mais, moi, ça me dépasse...)
Voilà mon angle d'attaque :
J'ai raisonné sur les différentes hauteurs des briques du mur, des briques situées sur la ligne plus basse jusqu'aux briques potentiellement situées sur la n-ième ligne (je dis potentiellement, car il n'est pas certain qu'il y en ait sur la n-ième ligne, c'est même le cas dans une unique configuration, et pour une brique, le cas où elles sont toutes les unes sur les autres)
On définit les n-listes (H1, H2,..., Hn) chaque Hi étant le nombre de briques présentes sur la i-ème ligne.
On doit avoir H1 + H2 + H3 + ... + Hn = n (puisqu'il y a n briques)
Et aussi H1 >= H2 >= ... >= Hn (car une rangée ne peut comporter plus de briques que celle du dessous, sinon problème)
Le nombre de n-listes ainsi définies donne la réponse au problème. Reste à les compter. Et là, c'est la stagnation totale.
On a déjà fait des exercices où il est question de compter des p-listes lorsque la somme de leurs p composantes est égale à un entier donné. Mais là, on leur rajoute en plus un ordre...
Bref, help me, please !
Bonsoir,
Juste pour info, considères tu qu'avec 2 briques on fait 2 murs, ou 3 ?
Car, en raisonnant sur les colonnes, on s'apercoit qu'on cherche en fait les n-uplet (x1,...,xn) avec xi dans N et tels que x1+...+xn = n.
Ca revient en fait à poser n séparations entre les n briques (le nombre de briques entre la (i+1)eme et la ieme séparation étant alors xi).
On trouve ainsi n parmi 2n possibilités.
Seulement, on n'a pas vraiment que des murs différents (par exemple celui qui consiste à empiler les n briques est compté n fois (selon sur quelle colonne celui ci est placé)).
Juste pour info, considères tu qu'avec 2 briques on fait 2 murs, ou 3 ?
Car, en raisonnant sur les colonnes, on s'apercoit qu'on cherche en fait les n-uplet (x1,...,xn) avec xi dans N et tels que x1+...+xn = n.
Ca revient en fait à poser n séparations entre les n briques (le nombre de briques entre la (i+1)eme et la ieme séparation étant alors xi).
On trouve ainsi n parmi 2n possibilités.
Seulement, on n'a pas vraiment que des murs différents (par exemple celui qui consiste à empiler les n briques est compté n fois (selon sur quelle colonne celui ci est placé)).
zb12 a écrit:On doit avoir H1 + H2 + H3 + ... + Hn = n (puisqu'il y a n briques)
L'indice n de
On aura:
Le nombre n de rangées varie de 1 à N.
Une solution consiste à trouver le nombre
Salut,
Bon, déjà, c'est pas trop clair.
Si, par exemple n=3, est-ce que tu es sûr qu'on considère comme un seul cas les deux murs avec 2 briques au sol et une posé dessus.
L'énoncé précise qu'une brique non au sol doit être posé sur une autre, mais là on peut poser celle du dessus soit sur celle de droite soit sur celle de gauche.
Perso, à la lecture de l'énoncé, j'aurais considéré que c'était deux "cas" différent, mais aprés, ça pose problème : avec 5 brique dont 3 au sol, est-ce qu'on peut mettre les deux du dessus non côte à côte ?
Bon, déjà, c'est pas trop clair.
Si, par exemple n=3, est-ce que tu es sûr qu'on considère comme un seul cas les deux murs avec 2 briques au sol et une posé dessus.
L'énoncé précise qu'une brique non au sol doit être posé sur une autre, mais là on peut poser celle du dessus soit sur celle de droite soit sur celle de gauche.
Perso, à la lecture de l'énoncé, j'aurais considéré que c'était deux "cas" différent, mais aprés, ça pose problème : avec 5 brique dont 3 au sol, est-ce qu'on peut mettre les deux du dessus non côte à côte ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si on a k briques posées au sol (k<=n), sans espace car on aurait alors plusieurs murs,
le nombre de k-uplets de somme n-k est
on ajoute

à vérifier car je trouve ça bien rapide ... (et faut voir si ça correspond bien à l'énoncé ...)
Deux exemples de murs (considérés bien-sûr comme différents) avec 8 briques (n=8 et k=4):


le nombre de k-uplets de somme n-k est
on ajoute
à vérifier car je trouve ça bien rapide ... (et faut voir si ça correspond bien à l'énoncé ...)
Deux exemples de murs (considérés bien-sûr comme différents) avec 8 briques (n=8 et k=4):


J'essaie une représentation graphique du mur (une brique posée est représentée par un "m", une brique qui cherche ses positions possibles est représentée par un "x".)
Pour poser 1 brique, je n'ai qu'un choix:
m
Pour poser 2 briques, j'ai 2 possibilités: (je suppose que la première est aussi à gauche que possible, on ne peut pas mettre la suivante plus à gauche qu'elle)
...........................x
mx.........ou...........m
Pour poser 3 briques, j'ai 4 possibilités:
.....................................................x
...................x................x................m
mmx.............mm...........mm...............m
Pour poser la 4 briques, j'ai 8 possibilités:
...................x.....................x.............x
mmmx...........mmm.............mmm......mmm
...............................................x
................x................x............m
mx............m...............m............m
mm...........mm...........mm............m
C'est pas des maths mais c'est bien utile, ça semble indiquer que ta solution est bonne.
Pour poser 1 brique, je n'ai qu'un choix:
m
Pour poser 2 briques, j'ai 2 possibilités: (je suppose que la première est aussi à gauche que possible, on ne peut pas mettre la suivante plus à gauche qu'elle)
...........................x
mx.........ou...........m
Pour poser 3 briques, j'ai 4 possibilités:
.....................................................x
...................x................x................m
mmx.............mm...........mm...............m
Pour poser la 4 briques, j'ai 8 possibilités:
...................x.....................x.............x
mmmx...........mmm.............mmm......mmm
...............................................x
................x................x............m
mx............m...............m............m
mm...........mm...........mm............m
C'est pas des maths mais c'est bien utile, ça semble indiquer que ta solution est bonne.
Frede a écrit:Pourquoi ne le seraient-ils pas ? Ils n'ont ni trou ni surplomb. (un surplomb, je pense que c'est une colonne avec un trou au niveau du sol)
alors mon résultat doit être bon ...
Un surplomb ça pourrait être des briques que ne seraient pas entièrement dans le plan vertical, ça permettrait d'entre mettre plus.
Un grand merci pour toutes vos réponses,
C'est vrai que l'énoncé n'est pas très explicite, mais que pense que tu as raison, Chan79 et que les deux murs que tu as dessinés sont acceptables. J'étais parti là dessus.
Je vois bien que ta réponse doit être juste, mais je n'arrive pas à comprendre le lien entre les Nn de mrif et ta réponse : poser un nombre k de briques au sol, et chercher le nombre de k-uplets tels que la somme de leurs composantes fasse n-k.
Pour la suite, j'ai compris.
Toi, ou mrif, ou quelqu'un d'autre peut-il m'éclairer ?
C'est vrai que l'énoncé n'est pas très explicite, mais que pense que tu as raison, Chan79 et que les deux murs que tu as dessinés sont acceptables. J'étais parti là dessus.
Je vois bien que ta réponse doit être juste, mais je n'arrive pas à comprendre le lien entre les Nn de mrif et ta réponse : poser un nombre k de briques au sol, et chercher le nombre de k-uplets tels que la somme de leurs composantes fasse n-k.
Pour la suite, j'ai compris.
Toi, ou mrif, ou quelqu'un d'autre peut-il m'éclairer ?
....Je ne peux pas répondre à la question posée mais je reviens car en y repensant, je vois une façon extrêmement simple de résoudre ce problème.
....On imagine qu'on a sous les yeux une colonne haute de N briques.
....N briques, ça implique N-1 points de contact entre elles.
....Pour chacun de ces N-1 points, on a deux possibilités: soit je casse et je commence une nouvelle colonne soit je ne casse pas et j'allonge la colonne en cours.
....Arrivé à la dernière, on a fait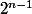 choix. A chaque ensemble de
choix. A chaque ensemble de 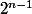 choix correspond un mur.
choix correspond un mur.
....Le nombre de murs possibles est donc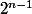
....On imagine qu'on a sous les yeux une colonne haute de N briques.
....N briques, ça implique N-1 points de contact entre elles.
....Pour chacun de ces N-1 points, on a deux possibilités: soit je casse et je commence une nouvelle colonne soit je ne casse pas et j'allonge la colonne en cours.
....Arrivé à la dernière, on a fait
....Le nombre de murs possibles est donc
Frede a écrit:....Je ne peux pas répondre à la question posée mais je reviens car en y repensant, je vois une façon extrêmement simple de résoudre ce problème.
....On imagine qu'on a sous les yeux une colonne haute de N briques.
....N briques, ça implique N-1 points de contact entre elles.
....Pour chacun de ces N-1 points, on a deux possibilités: soit je casse et je commence une nouvelle colonne soit je ne casse pas et j'allonge la colonne en cours.
....Arrivé à la dernière, on a prisdécisions. A chaque ensemble de
décisions correspond un mur.
....Le nombre de murs possibles est donc
Excellente idée ! :++:
Le nombre de murs n'est autre que le nombre de parties de l'ensemble {1;2;3;...n-1}.
Donc, c'est
En y repensant, la solution n'est pas tout à fait satisfaisante. On me devrait pas avoir à compter en double les murs symétriques. (voir le dessin de Chan)
Mais comment faire pour les dénombrer, et les enlever?
Désolée, de rederanger ^^'
On pourrait tout diviser par 2, et rajouter les murs présentant une symétrie axiale ? Comme les murs rectangulaires... En fait, j'en rajoute mais je sais toujours pas comment faire pour les denombrer...
Mais comment faire pour les dénombrer, et les enlever?
Désolée, de rederanger ^^'
On pourrait tout diviser par 2, et rajouter les murs présentant une symétrie axiale ? Comme les murs rectangulaires... En fait, j'en rajoute mais je sais toujours pas comment faire pour les denombrer...
zb12 a écrit:En y repensant, la solution n'est pas tout à fait satisfaisante. On me devrait pas avoir à compter en double les murs symétriques. (voir le dessin de Chan)
Mais comment faire pour les dénombrer, et les enlever?
Désolée, de rederanger ^^'
On pourrait tout diviser par 2, et rajouter les murs présentant une symétrie axiale ? Comme les murs rectangulaires... En fait, j'en rajoute mais je sais toujours pas comment faire pour les denombrer...
et les murs ayant 2 ou ou plusieurs colonnes côte à côte de même hauteur?
C'est ça qui n'est pas très clair, mais bon. Pour ça, il faudrait aussi une définition claire du "trou"... Est-ce qu'un trou, ça doit être "fermé" sur le dessus ? Si un trou correspond à toute colonne moins haute que ses 2 voisines, nos murs tout crénelés sont interdits...
Mais admettons qu'on a droit à toutes sortes de murs, construits de manière totalement chaotique (on ne nous donne pas le nom de l'agence contactée pour la construction...) sans trou, ni surplomb.
Mais il demeure que les murs que Chan a dessinés sont identiques (il suffit pour l'observateur de passer de l'autre côté), il faudrait donc les enlever...
Mais admettons qu'on a droit à toutes sortes de murs, construits de manière totalement chaotique (on ne nous donne pas le nom de l'agence contactée pour la construction...) sans trou, ni surplomb.
Mais il demeure que les murs que Chan a dessinés sont identiques (il suffit pour l'observateur de passer de l'autre côté), il faudrait donc les enlever...
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
