Bonjour,
Considérons H=L2([0,1],R) muni du produit scalaire usuel, et phi l'application linéaire qui à toute fonction f dans H associe son intégrale entre 0 et 1.
Il est alors demandé de déterminer le noyau de Ker phi et son orthogonal.
Est-il possible de déterminer explicitement le noyau de phi ? Je me suis contenté de dire que Ker phi c'est l'ensemble des fonctions dont l'intégrale est nulle entre 0 et 1 (car je ne vois pas comment aller plus loin).
Et je conjecture que l'orthogonal de Ker phi est réduit aux fonctions constantes : est-ce vrai ? et si oui, comment peut-on le montrer ?
Je vous remercie par avance de votre aide.
Bonne journée !
Exo d'analyse fonctionnelle
3 messages
- Page 1 sur 1
Re: Exo d'analyse fonctionnelle
Salut,
Déterminer le noyau de phi plus explicitement qu'en disant que l'intégrale de 0 à 1 doit être nulle, ça m'étonnerais fort que ce soit possible (vu que ça fait un énorme tas de fonctions).
Et concernant l'orthogonal, c'est bien l'ensemble des fonctions constantes (donc un s.e.v. de dimension 1 de H) et ça provient du fait que ta forme linéaire phi, c'est f -> <f|1> (produit scalaire) : son noyau est donc l'hyperplan (fermé) et
et 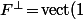)
Déterminer le noyau de phi plus explicitement qu'en disant que l'intégrale de 0 à 1 doit être nulle, ça m'étonnerais fort que ce soit possible (vu que ça fait un énorme tas de fonctions).
Et concernant l'orthogonal, c'est bien l'ensemble des fonctions constantes (donc un s.e.v. de dimension 1 de H) et ça provient du fait que ta forme linéaire phi, c'est f -> <f|1> (produit scalaire) : son noyau est donc l'hyperplan (fermé)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
