Bonjour,
Je planche sur la question suivante et j'aurai besoin d'un peut d'aide :
soit b(t) = 1/sqrt(2pi) integrale_sur_R ( ((x^2+1)/(x^4 +x^2+2)) * exp(ixt) dx)
montrer que cette fonction appartient a L1(R) inter Linfini(R)
Pour Linfini(R) pas de problème. Mais je n'arrive pas a montrer quelle appartient L1(R).
Désolé pour l'expression dégeux de ma fonction mais je ne sais pas introduire de symboles mathématiques
Merci d'avance!
Analyse fonctionnelle
10 messages
- Page 1 sur 1
par girdav » 23 Mai 2010, 08:07
Bonjour,
la fonction est positive : il suffit de montrer que l'intégrale de la fonction sur
est finie, ce qui peut se faire par comparaison ou équivalent.
la fonction est positive : il suffit de montrer que l'intégrale de la fonction sur
par zephira » 23 Mai 2010, 09:01
bonjour, il s'agit de montrer que l'intégrale de |b(t)| est convergente et non pas que b(t) est bien définie. or je pensais initialement majorer l'intégrale de |b(t)| en rentrant le modle dans la deuxième intégrale. Malheureusement quand je fais cela je me retrouve ac un module de exp(ixt) qui vaut un et donc je n'ai plus de termes en t. donc l'intégrale diverge..
par girdav » 23 Mai 2010, 09:13
Désolé j'ai mal lu l'énoncé...
Je n'ai pas essayé de calculer l'intégrale avec les résidus (je ne pense pas que ça soit comme cela que l'on nous demande de procéder).
Je n'ai pas essayé de calculer l'intégrale avec les résidus (je ne pense pas que ça soit comme cela que l'on nous demande de procéder).
par zephira » 23 Mai 2010, 09:53
je ne pense pas qu'il y ait besoin de calculer les résidus, cet exos étant tiré d'une annale d'analyse fonctionnelle. Je pensais peut etre à une IPP pour faire sortir un t de exp(ixt) (lorsqu'on intègre par rapport à dx), mais je ne m'en sors pas trop..
par Ben314 » 23 Mai 2010, 13:40
Salut,
 = \frac{1}{\sqrt{2\pi}}\int_{\bb R} F(x)\exp(itx)\,dx)
où =\frac{x^2+1}{x^4 +x^2+2})
est une fraction rationelle définie sur 
tout entier et de "degrés" -2 (en définissant le "degrés" de 
comme étant égal à -\deg(Q))
)
Cela implique que
et 
sont définis sur tout entier et de "degrés" respectif -3 et -4 (en utilisant le fait que ^{\prime}=\frac{P^{\prime}Q-PQ^{\prime}}{Q^2})
).
A noter : il n'est pas utile du tout de calculer et ...
Pour tout réel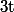
non nul, en faisant des intégrations par parties, on a :
\ <br />=\ \frac{1}{\sqrt{2\pi}}\left[F(x)\frac{\exp(ixt)}{it}\right]_{x=-\infty}^{x=+\infty}\,<br />-\frac{1}{\sqrt{2\pi}}\int_{\bb R} F^{\prime}(x)\frac{\exp(ixt)}{it}\,dx\<br />=\ \frac{i}{t\sqrt{2\pi}}\int_{\bb R} F^{\prime}(x)\exp(ixt)\,dx)
\frac{\exp(ixt)}{it}\right]_{x=-\infty}^{x=+\infty}\,<br />-\frac{i}{t\sqrt{2\pi}}\int_{\bb R} F^{\prime\prime}(x)\frac{\exp(ixt)}{it}\,dx\<br />=\ -\frac{1}{t^2\sqrt{2\pi}}\int_{\bb R} F^{\prime\prime}(x)\exp(ixt)\,dx)
On en déduit que
|\ <br />\leq\ \frac{1}{t^2\sqrt{2\pi}}\int_{\bb R} |F^{\prime\prime}(x)|\,dx\ <br />=\frac{\rm Cst}{t^2})
et donc que la fonction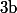
est absolument intégrable au voisinage de l'infini.
Cela implique que
A noter : il n'est pas utile du tout de calculer
Pour tout réel
On en déduit que
et donc que la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par zephira » 23 Mai 2010, 18:59
merci beaucoup! Ca parait tout de suite très facile dit comme ca :)
Ps : Comment écris tu les intégrales & les quotients?
Ps : Comment écris tu les intégrales & les quotients?
par Ben314 » 23 Mai 2010, 21:41
C'est du "mimeTeX" (une version un peu zarby de LateX) :
Tu en trouvera une descripition ici.
Tu peut cliquer sur "citer" en dessous des messages qui contiennent ce type de formule pour voir comment elles ont été codées.
Tu en trouvera une descripition ici.
Tu peut cliquer sur "citer" en dessous des messages qui contiennent ce type de formule pour voir comment elles ont été codées.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :