Exo algebre- Gauss / Determinant
26 messages
- Page 1 sur 2 - 1, 2
Exo algebre- Gauss / Determinant
Bonjour à tous.
J'ai fait un exercice d'algebre, dont voici l'énoncé:
Soit a appartient à R. Résoudre dans R^3 le système:
ax+y+z=1
x+ay+z=1
x+y+az=1
d'abord par la méthode de Gauss, puis par la méthode des déterminants.
Le problème est que j'ai fait faux, puisque j'ai deux résultats différents avec les méthodes...
J'aimerais donc savoir quel résultat est faux; d'ailleurs, les deux le sont peut etre.
Dans ce cas j'aimerais une explication de la méthode sur laquelle j'ai fait faux, parce qu'il me semblait avoir fait ça assez correctement.
Avec la méthode de Gauss, je trouve:
S={(-2a/(1-a),1/(1-a),1/(1-a),a appartient à R\{1}}
Avec la méthode des déterminants, je trouve:
S={(a²-1)/(a^3-a),(a²-1)/(a^3-a),(a²-2a+1)/(a^3-a), a appartient à R\{1}}
D'ailleurs plus je relis mon résultat avec la méthode des déterminants, plus elle me semble fausse, et de meme avec la methode de Gauss.
Pourtant, je ne vois pas ou j'ai pu commetre une erreur.
Merci d'avance
J'ai fait un exercice d'algebre, dont voici l'énoncé:
Soit a appartient à R. Résoudre dans R^3 le système:
ax+y+z=1
x+ay+z=1
x+y+az=1
d'abord par la méthode de Gauss, puis par la méthode des déterminants.
Le problème est que j'ai fait faux, puisque j'ai deux résultats différents avec les méthodes...
J'aimerais donc savoir quel résultat est faux; d'ailleurs, les deux le sont peut etre.
Dans ce cas j'aimerais une explication de la méthode sur laquelle j'ai fait faux, parce qu'il me semblait avoir fait ça assez correctement.
Avec la méthode de Gauss, je trouve:
S={(-2a/(1-a),1/(1-a),1/(1-a),a appartient à R\{1}}
Avec la méthode des déterminants, je trouve:
S={(a²-1)/(a^3-a),(a²-1)/(a^3-a),(a²-2a+1)/(a^3-a), a appartient à R\{1}}
D'ailleurs plus je relis mon résultat avec la méthode des déterminants, plus elle me semble fausse, et de meme avec la methode de Gauss.
Pourtant, je ne vois pas ou j'ai pu commetre une erreur.
Merci d'avance
Les deux sont faux, à la vue du système on sait que l'on doit trouver des solutions telles que x=y=z.
De plus il faut discuter les valeurs de , si a=-2 on voit que la somme des 3 équations sera nulle donc les 3 équations seront liées ... Cette valeur a=-2 est à traiter à part (elle rend le déterminant nul)
, si a=-2 on voit que la somme des 3 équations sera nulle donc les 3 équations seront liées ... Cette valeur a=-2 est à traiter à part (elle rend le déterminant nul)
Tout calcul fait tu dois trouver il me semble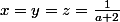 pour
pour  différent de
différent de 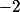 et
et 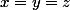 pour
pour 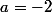
De plus il faut discuter les valeurs de
Tout calcul fait tu dois trouver il me semble
J'ai peut etre fait faux vers le début avec la méthode de Gauss..
J'arrive à ceci:
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
Et je dis que c'est équivalent à:
x+ay+z=1
y-z=0 (car on a y+((a-1)/(1-a))z=0 et (a-1)/(1-a)=-1)
-ay+z=1
Est ce que j'ai déjà faux à cet endroit ?
Par contre, concernant la méthode des déterminants, je ne vois vraiment pas a quel stade j'ai pu faire une erreur..
On doit utiliser les formules avec le systeme initial non?
J'obtiens pour déterminant de M: a^3-a peut etre ais je deja faux a ce stade?
Pour le trouver, j'ai fait:
det(M)=a*(a²-1)-(1-a)+(1-a)
J'arrive à ceci:
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
Et je dis que c'est équivalent à:
x+ay+z=1
y-z=0 (car on a y+((a-1)/(1-a))z=0 et (a-1)/(1-a)=-1)
-ay+z=1
Est ce que j'ai déjà faux à cet endroit ?
Par contre, concernant la méthode des déterminants, je ne vois vraiment pas a quel stade j'ai pu faire une erreur..
On doit utiliser les formules avec le systeme initial non?
J'obtiens pour déterminant de M: a^3-a peut etre ais je deja faux a ce stade?
Pour le trouver, j'ai fait:
det(M)=a*(a²-1)-(1-a)+(1-a)
Ah oui effectivement!
Moi j'ai agi en pensant que cela ressemblait au produit mixte, les formules et tout ça, donc c'est effectivement comme le produit mixte pour le premier et le troisieme det, mais pas pour celui du milieu...
Au passage, qu'en est-il pour la méthode de Gauss? Les étapes que j'ai proposé sont elles déjà fausses ou ma faute vient elle plus loin?
Moi j'ai agi en pensant que cela ressemblait au produit mixte, les formules et tout ça, donc c'est effectivement comme le produit mixte pour le premier et le troisieme det, mais pas pour celui du milieu...
Au passage, qu'en est-il pour la méthode de Gauss? Les étapes que j'ai proposé sont elles déjà fausses ou ma faute vient elle plus loin?
Je ne sais pas ou se situe l'erreur dans ce cas.. Voilà ce que j'ai fait:
(A chaque fois que je saute de ligne, c'est qu'il y a une equivalence)
ax+y+z=1
x+ay+z=1
x+y+az=1
x+ay+z=1
x+y+az=1
ax+y+z=1
x+ay+z=1
(1-a)y+(a-1)z=0
(1-a²)y+(1-a)z=1-a
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
x+ay+z=1
y-z=0
-ay+z=1
Ou est l'erreur?
(A chaque fois que je saute de ligne, c'est qu'il y a une equivalence)
ax+y+z=1
x+ay+z=1
x+y+az=1
x+ay+z=1
x+y+az=1
ax+y+z=1
x+ay+z=1
(1-a)y+(a-1)z=0
(1-a²)y+(1-a)z=1-a
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
x+ay+z=1
y-z=0
-ay+z=1
Ou est l'erreur?
Jusque la c'est bon :
x+ay+z=1
(1-a)y+(a-1)z=0
(1-a²)y+(1-a)z=1-a
Ensuite la ligen en rouge je vois pas d'où ca sort.
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
De plus ca ne correspond plus à la méthode de Gauss qui consiste à trianguler le système ... il faut donc faire disparaitre le terme en y dans la dernière ligne.
x+ay+z=1
(1-a)y+(a-1)z=0
(1-a²)y+(1-a)z=1-a
Ensuite la ligen en rouge je vois pas d'où ca sort.
x+ay+z=1
(1-a)y+(a-1)z=0
-ay+z=1
De plus ca ne correspond plus à la méthode de Gauss qui consiste à trianguler le système ... il faut donc faire disparaitre le terme en y dans la dernière ligne.
Effectivement, la ligne en rouge est fausse, j'ai voulu simplifier par 1-a..
Mais vu que ce n'est pas possible, comment puis je rendre le coefficient de y égal à 1 dans la deuxieme équation et donc le supprimer dans la troisieme ?
(Le calcul ici n'etait pas fini, je mettais jusqu'a l'endroit ou j'avais un doute)
Mais vu que ce n'est pas possible, comment puis je rendre le coefficient de y égal à 1 dans la deuxieme équation et donc le supprimer dans la troisieme ?
(Le calcul ici n'etait pas fini, je mettais jusqu'a l'endroit ou j'avais un doute)
Arnaud-29-31 a écrit:Les deux sont faux, à la vue du système on sait que l'on doit trouver des solutions telles que x=y=z.
De plus il faut discuter les valeurs de, si a=-2 on voit que la somme des 3 équations sera nulle donc les 3 équations seront liées ... Cette valeur a=-2 est à traiter à part (elle rend le déterminant nul)
Tout calcul fait tu dois trouver il me semblepour
différent de
et
pour
Bien-sûr,si a=1, il y a une infinité de solutions
Si, la simplification par (1-a) est possible sur la deuxième ligne ... ca donne y-z = 0 en deuxième ligne.
Oui mais après je suis bloqué en troisieme ligne...
J'ai en simplifiant (a²-a+2)z=0 et je n'arrive pas à le mettre en coefficient 1.
Bien-sûr,si a=1, il y a une infinité de solutions
Quand on remplace a par 1 dans le systeme initial, c'est évident.
Mais autrement, comment le déduit tu avec des calculs?
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
