Non.
U2= U(2-1) + 2 * (-1)^2 = U1 + 2 = -1 + 2 = 1.
Exerices suites
30 messages
- Page 2 sur 2 - 1, 2
"tu me l'a pas mis!"
Patoche, je ne suis pas là pour faire tes exercice à ta place. En revanche, je suis d'accord pour t'aider. J'ai en effet sauté la ligne intermédiaire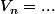
Mais j'ai une écrit :
si n pair :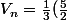^{n/2})
et :
si n impair :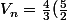^{(n-1)/2})
Ce n'est quand même pas si difficile de mettre ces 2 lignes immédiatement l'une en-dessous de l'autre dans une même formule !
Nicolas
Patoche, je ne suis pas là pour faire tes exercice à ta place. En revanche, je suis d'accord pour t'aider. J'ai en effet sauté la ligne intermédiaire
Mais j'ai une écrit :
si n pair :
et :
si n impair :
Ce n'est quand même pas si difficile de mettre ces 2 lignes immédiatement l'une en-dessous de l'autre dans une même formule !
Nicolas
30 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
