quaresma a écrit:tu es sur de toi QUIDAM ?
Autant qu'on peut l'être ! C'est-à-dire pas à 100% ! Tu dois savoir qu'en maths, on n'est jamais sûr à 100%, car personne (pas moi en tous cas !) n'est à l'abri d'une erreur ! Mais il y a souvent moyen de vérifier ! D'abord, on va voir si le tableau de variation qui découlera de ce calcul de dérivée est bien conforme à la courbe ! Ensuite, j'ai une deuxième méthode sous le coude pour calculer la dérivée.
=\frac{4x^3-x^2}{1-x})
Je divise

par 1-x :
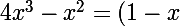\times(-4x^2-3x-3)+3)
Ensuite :
=\frac{4x^3-x^2}{1-x}=\frac{(1-x)\times(-4x^2-3x-3)+3}{1-x})
=\frac{(1-x)\times(-4x^2-3x-3)}{1-x}+\frac{3}{1-x}=-4x^2-3x-3+\frac{3}{1-x})
=-4x^2-3x-3+\frac{3}{1-x})
Ensuite, c'est tout facile de calculer la dérivée :
=-8x-3+\frac{3}{(1-x)^2})
=\frac{(-8x-3)(1-x)^2+3}{(1-x)^2})
=\frac{(-8x-3)(1-2x+x^2)+3}{(1-x)^2})
=\frac{-8x^3+13x^2-2x}{(1-x)^2})
Comme j'obtiens la même chose qu'avec l'autre méthode, je suis quasiment sûr que je n'ai pas fait d'erreur ! Mais va savoir !
quaresma a écrit:et pr le domaine de def comment faire ?
Pour le domaine de définition, rien de plus simple. Tout est possible sauf éventuellement la division, si le dénominateur est nul ! Donc le domaine est
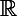
duquel on a enlevé l'unique réel qui annulle le dénominateur : 1 !
quaresma a écrit:le tableau de variation doit être chaud a construire aussi non ?
Non ! Pas dur ! Essaye donc, tu verras bien !
