Exercice sur les nombres complexes
16 messages
- Page 1 sur 1
 Exercice sur les nombres complexes
Exercice sur les nombres complexes
a un réel différents de pi +2kpi (k appartenant à N) et b est un réel. Exprimer en fonction de a et b la partie réelle et imaginaire du nombre complexe suivant : e^i*b -1 / e^i^a +1
Re: Exercice sur les nombres complexes
Bonjour,
2 remarques:
1)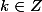
2) je crois qu'il manque des parenthèses OBLIGATOIRES
Où en es-tu dans tes cogitations?
2 remarques:
1)
2) je crois qu'il manque des parenthèses OBLIGATOIRES
Où en es-tu dans tes cogitations?
Re: Exercice sur les nombres complexes
Bonjour,
Oui désolée pour ses erreurs d'énoncé, je l'ai écrit rapidement :
a un réel différent de pi +2kpi (k appartenant à Z) et b est un réel. Exprimer en fonction de a et b la partie réelle et imaginaire du nombre complexe suivant : (e^i*b -1) / (e^i^a +1)
J'ai essayé de multiplié par le conjugué, mais j'obtiens une expression plus compliqué...
Oui désolée pour ses erreurs d'énoncé, je l'ai écrit rapidement :
a un réel différent de pi +2kpi (k appartenant à Z) et b est un réel. Exprimer en fonction de a et b la partie réelle et imaginaire du nombre complexe suivant : (e^i*b -1) / (e^i^a +1)
J'ai essayé de multiplié par le conjugué, mais j'obtiens une expression plus compliqué...
Re: Exercice sur les nombres complexes
pense à utiliser la technique de l'angle moitié, alors c'est très rapide et pas compliqué
Re: Exercice sur les nombres complexes
Je l'ai vu en cours, mais avec des expressions contenant pi, je ne pensais pas que l'on pouvais le faire avec des lettres, je vais essayer !
Re: Exercice sur les nombres complexes
J'ai obtenu ce résultat :
e^i((ba-2pi)/2)*(cos((ib)/2)/sin((ia)/2)
J'ai une dernière question, je ne sais pas différencier la partie imaginaire de la partie réelle, car me disant que dans chaque fonction, ayant un nombre imaginaire qui y apparaît, elles sont toutes imaginaires ?
e^i((ba-2pi)/2)*(cos((ib)/2)/sin((ia)/2)
J'ai une dernière question, je ne sais pas différencier la partie imaginaire de la partie réelle, car me disant que dans chaque fonction, ayant un nombre imaginaire qui y apparaît, elles sont toutes imaginaires ?
Re: Exercice sur les nombres complexes
je ne comprends pas ton résultat,
à la fin, tu devrais trouver
}{cos(\dfrac{a}{2})} \left[sin (\dfrac{a-b}{2})+i\, cos(\dfrac{a-b}{2})\right])
montre un peu ton développement
à la fin, tu devrais trouver
montre un peu ton développement
Re: Exercice sur les nombres complexes
C'est la méthode que j'ai vu en cours : https://photos.app.goo.gl/zt8nYunuxxzjoK757
Re: Exercice sur les nombres complexes
ta 2e ligne ne va pas, revois un peu ton développement car il y a plusieurs erreurs, par exemple
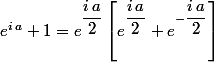
Re: Exercice sur les nombres complexes
J'ai refait le calcul et je n'obtiens toujours pas le bon résultat. https://photos.app.goo.gl/yDbFj6dXMxxpFB1e9
Re: Exercice sur les nombres complexes
tu y es presque
l'erreur vient d'ici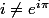 ; développe et tu verras !!
; développe et tu verras !!
l'erreur vient d'ici
Re: Exercice sur les nombres complexes
Ah oui c'est égal à e^pi/ : https://photos.app.goo.gl/XU3bk61LutPHrJkj7
Re: Exercice sur les nombres complexes
Chloé102003 a écrit:Ah oui c'est égal à e^pi/ : https://photos.app.goo.gl/XU3bk61LutPHrJkj7
mais ça semble correct dans ton document
ensuite
de même
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
