Exercice Fonction 2 variables

par **Ben314** » 10 Jan 2019, 21:56

Pour le contre exemple, c'est assez immédiat :

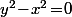
donne

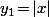
et

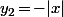
si on fixe

.

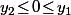
Après, concernant la 2em question, la réponse doit être OUI si on suppose

et

analytiques vu que dans ce cas

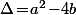
va aussi l'être et, vu que par hypothèse

est positif sur

, c'est qu'au points éventuels points

tels que

on va avoir

avec

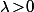
et

pair ce qui permet d'avoir une détermination analytique des deux racines racines de

au voisinage de

.

Si on ne suppose

et

"que"

et pas analytique, j'ai l'impression que ça marche pareil, mais je suis pas sûr à 100% . . .

par **aviateur** » 10 Jan 2019, 22:27

Rebonjour
D'accord @ben.
Par contre si la fonction n'est pas analytique c'est pas clair pour moi si on a un zéro non isolé.