Comment majorer un fonction à deux variables?

[waddle30]

bonsoir tout le monde.
Le calcule de limite d'un fonction à deux variables revient souvent à la majorer mais est-ce qu'il il y une méthode générale?
par exemple comment majore t-on:
f(x,y)=(x²+y²)/(|x|+|y|)
f(x,y)=(x²y²)/(x²+y²)

il faut souvent utiliser l'ingégalité 2aba²+b²
mais la je ne vois pas trop.

[busard_des_roseaux]

Bonjour,

pour les cas d'école, on passe en coordonnées polaires. on utilise le fait que sinus et cosinus (réels) sont majorés en valeurs absolues, par 1

exemple 1

dans le 1er cadran



exemple2



pour les cas standards de fonctions de plusieurs variables, on majore l'application différentielle, quand elle est de classe C1 (continuement différentiable) , localement sur un compact de . On utilise l'inégalités des accroissements finis , qui est valable dans un espace de Banach

[waddle30]

ok merci mais sans utiliser les coordonnée polaires comment on fait?
comment on montre que
|(x²y²)/(x²+y²)|<2|x| ?

[busard_des_roseaux]

[quote="waddle30"]ok merci mais sans utiliser les coordonnée polaires comment on fait?
comment on montre que
|(x²y²)/(x²+y²)|2 , ce qui se voit immédiatement en polaires

[waddle30]

|f(x,y)|=|(x²y²)|/|(x²+y²)<2|xy|/(|x|+|y|)=2|x|
c'est faux ?

[ffpower]

oui c'est faux
(fais x=y pour voir)

[Cryptocatron-11]

il faut souvent utiliser l'ingégalité 2aba²+b²

tu parles de l'inégalité et donc que ?

[busard_des_roseaux]

ok merci mais sans utiliser les coordonnée polaires comment on fait?
comment on montre que
|(x²y²)/(x²+y²)|<2|x| ?

on t'a dit ce qu'il y avait à faire, tu ne le fais pas :petard:

[waddle30]

tu parles de l'inégalité et donc que ?

oui c'est bien sa

x=y=10 \frac{10 000}{200}=50 < 20 on t'a dit ce qu'il y avait à faire, tu ne le fais pas

dsl mais comme je ne suis pas trop à l'aise avec les coordonnées polaires j’essaye de trouver une autre méthode :bad:

[Cryptocatron-11]

bonsoir tout le monde.
Le calcule de limite d'un fonction à deux variables revient souvent à la majorer mais est-ce qu'il il y une méthode générale?
par exemple comment majore t-on:
f(x,y)=(x²y²)/(x²+y²)

Tu ne précises pas au voisinage de quels points tu souhaites connaitre la limite mais admettons que ça soit en (0,0). Si je ne m'abuse on peut écrire que
Or
on fait de même pour y
On arrive à qui tend vers 0.

(Je ne suis pas sur que ça soit correcte car je me pose les mêmes questions)

[bentaarito]

Bonjour,

pour les cas d'école, on passe en coordonnées polaires. on utilise le fait que sinus et cosinus (réels) sont majorés en valeurs absolues, par 1

exemple 1

dans le 1er cadran



exemple2



pour les cas standards de fonctions de plusieurs variables, on majore l'application différentielle, quand elle est de classe C1 (continuement différentiable) , localement sur un compact de . On utilise l'inégalités des accroissements finis , qui est valable dans un espace de Banach

ton n'est pas dans

[busard_des_roseaux]

ton n'est pas dans

on teste dans le 1er quadrant du cercle (ou du disque) et après c'est vérifié sur tout le cercle en changeant en ou en

[Cryptocatron-11]

Du coup c'est juste ou pas mon truc ?

[waddle30]

on t'a dit ce qu'il y avait à faire, tu ne le fais pas :petard:

ce n'est pas moi qui le dit j'ai trouver sa sur ce site :
http://mp.cpgedupuydelome.fr/mesexos.php?idChap=38
cf(l'exo 3)

Du coup c'est juste ou pas mon truc ?

je pense que c'est bon mais personne pour une confirmation ??

[busard_des_roseaux]

pour déterminer une limite, on travaille sur des conditions suffisantes , pas nécessaires.

donc , tu peux écrire des milliers d'inégalités, qui ne sont pas vraies globalement mais suffisantes, dans un voisinage de zéro pour calculer une limite.

you see what I mean ?

l'intérêt des coordonnées polaires, c'est qu'elles donnent la meilleure majoration possible, obtenue en général pour une direction particulière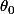 , mais parfois, on envisage la restriction de la fonction à une courbe particulière pour des besoins spécifiques. Par exemple, tu peux restreindre f(x,y) au graphe de 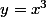si ça te chante...

je signale aussi la dérivée au sens de Gâteaux ...dont les travaux ont été repris par Wiener pour le mouvement brownien.

[Doraki]

Or

:/

Comme (x-y)² >= 0, x²+y² >= 2xy, et donc pour tout x y (non tous les deux nuls),
|f(x,y)| = x²y² / (x²+y²) <= x²y² / 2|xy| = |xy|/2 <= (x²+y²)/4.

Donc f(x,y) tend vers 0 quand (x²+y²) tend vers 0 (quand (x,y) tend vers (0,0))

[Skullkid]

Du coup c'est juste ou pas mon truc ?

Salut, non ça ne va pas. À un moment tu dis que |x| <= |x²+y²|, ce qui est faux par exemple si |x| < 1 et y = 0. La première correction donnée pour l'exo 3d sur le site de waddle30 est fausse aussi si on n'impose pas de conditions sur x et y (l'inégalité est valable sur un voisinage de (0,0), donc elle est satisfaisante pour calculer la limite, mais elle reste fausse en général), comme l'ont déjà fait remarquer busard_des_roseaux et ffpower.

Si on veut une solution sans coordonnées polaires on peut faire par exemple .

[Cryptocatron-11]

Effectivement ça marchait que pour |x|² je viens dm'en rendre compte ...

Merci pour votre aide. Du coup l'inégalité de waddle pouvait marcher ici