Exercice continuité

par **bayzou** » 16 Jan 2015, 23:10

La fonction suivante est-elle prolongeable par continuité en 0 f(x)=1/x - 1/sinx ? Son prolongement est-il de classe 1 ? quelqu'un peut m'aider :p :ptdr: merci

par **Monsieur23** » 16 Jan 2015, 23:32

Aloha,

As-tu tracé la courbe ? À ton avis, prolongeable ou pas ? Par quoi ?

par **Manny06** » 17 Jan 2015, 08:35

bayzou a écrit:La fonction suivante est-elle prolongeable par continuité en 0 f(x)=1/x - 1/sinx ? Son prolongement est-il de classe 1 ? quelqu'un peut m'aider :p :ptdr: merci

tu peux aussi faire un développement limité de sinx au voisinage de 0

par **bayzou** » 17 Jan 2015, 19:09

Manny06 a écrit:tu peux aussi faire un développement limité de sinx au voisinage de 0

elle est 2pi périodique mais je ne sais pas si elle est prolongeable
je fais un DL d'ordre cb en (0)???

par **Manny06** » 17 Jan 2015, 20:14

bayzou a écrit:elle est 2pi périodique mais je ne sais pas si elle est prolongeable
je fais un DL d'ordre cb en (0)???

elle n'est pas périodique
il suffit de faire un DL à l'ordre 3

par **bayzou** » 17 Jan 2015, 20:18

Manny06 a écrit:elle n'est pas périodique
il suffit de faire un DL à l'ordre 3

OK mais pourquoi un DL d'ordre 3 j'aimerais comprendre merci !

par **Manny06** » 17 Jan 2015, 20:31

bayzou a écrit:OK mais pourquoi un DL d'ordre 3 j'aimerais comprendre merci !

parce qu'avec le denominateur xsinx qui est d'ordre 2 il faut aller jusqu'à l'ordre 3 au numérateur pour pouvoir simplifier et obtenir une limite finie

par **bayzou** » 17 Jan 2015, 20:50

Manny06 a écrit:parce qu'avec le denominateur xsinx qui est d'ordre 2 il faut aller jusqu'à l'ordre 3 au numérateur pour pouvoir simplifier et obtenir une limite finie

donc je fais un dl de SINX-x sur xsinx ?

par **Manny06** » 17 Jan 2015, 21:03

bayzou a écrit:donc je fais un dl de SINX-x sur xsinx ?

oui c'est çà

par **zygomatique** » 17 Jan 2015, 22:59

salut

donc

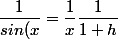
puis dl de

puis f(x) = ...

par **Pythales** » 18 Jan 2015, 10:16

bayzou a écrit:La fonction suivante est-elle prolongeable par continuité en 0 f(x)=1/x - 1/sinx ? Son prolongement est-il de classe 1 ? quelqu'un peut m'aider :p :ptdr: merci

et applique 2 fois l'Hopital

par **bayzou** » 18 Jan 2015, 11:34

Pythales a écrit: et applique 2 fois l'Hopital

ok merci de l'aide! je vais faire ça de suite mais j'ai pas fait le théorème de l'hôpital en cours même si je sais qu'il s'applique en 0/0 ET infini sur infini et qu'il faut faut dériver y a t-il un autre moyen pour la 2nd question?

par **bayzou** » 18 Jan 2015, 11:39

bayzou a écrit:ok merci de l'aide! je vais faire ça de suite mais j'ai pas fait le théorème de l'hôpital en cours même si je sais qu'il s'applique en 0/0 ET infini sur infini et qu'il faut faut dériver y a t-il un autre moyen pour la 2nd question?

je n'arrive pas à comprendre le Dl de zygomatique après sin(x) pour sin(x) j'ai la même chose mais après je comrend plus rien

par **zygomatique** » 18 Jan 2015, 12:09

zygomatique a écrit:salut

donc

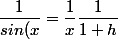
puis dl de

puis f(x) = ...

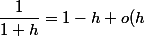avec

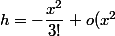donc

il suffit alors de calculer f(x) ...

par **bayzou** » 18 Jan 2015, 13:11

zygomatique a écrit: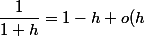

avec

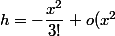donc

il suffit alors de calculer f(x) ...

mais f(x) c'est pas ça ? moi j'ai calculé le dl de x sinx et séparément sin(x)-x et de former un quotient ? j'ai sûrement faux mais j'essaye de comprendre votre méthode mais je comprend pas comment de 1/sin(x) on passe à la fonction merci !

par **zygomatique** » 18 Jan 2015, 13:18

bayzou a écrit:mais f(x) c'est pas ça ? moi j'ai calculé le dl de x sinx et séparément sin(x)-x et de former un quotient ? j'ai sûrement faux mais j'essaye de comprendre votre méthode mais je comprend pas comment de 1/sin(x) on passe à la fonction merci !

mais un peu de sérieux !!!!

par **bayzou** » 18 Jan 2015, 13:22

zygomatique a écrit:mais un peu de sérieux !!!!

moi je veux bien faire ce que vous faites mais le DL de 1/X il n'existe pas ?

par **zygomatique** » 18 Jan 2015, 13:27

bayzou a écrit:moi je veux bien faire ce que vous faites mais le DL de 1/X il n'existe pas ?

:mur:

mais on n'en a rien à péter du dl de 1/x .... puisqu'il n'existe pas !!!

par **bayzou** » 18 Jan 2015, 13:30

zygomatique a écrit::mur:

mais on n'en a rien à péter du dl de 1/x .... puisqu'il n'existe pas !!!

bah alors comment je fait pour me ramener à f(x) désolé j'ai du mal à comprendre tout ça :hum:

par **zygomatique** » 18 Jan 2015, 13:33

désolé si tu ne sais pas lire ...

voir à 12h09 et à 13h18

Exercice continuité

exercice continuité

Qui est en ligne