Bonsoir à toutes/tous,
voilà un exercice dont le but est de calculer l'intégrale de Gauss bien connue
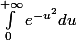
, et dont je ne saisis pas un passage de la correction.
On considère la fonction
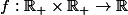
définie par
 = \frac{e^{-xt^2}}{t^2+1})
On pose
 = \int_{0}^{+ \infty}f(x,t) dt)
On montre en premier lieu que la fonction

est bien définie, continue (d'après le théorème de continuité des intégrales à paramètres) sur

puis dans la foulée que
 = \frac{\pi}{2})
et que
 = 0)
Puis on montre que F est dérivable sur
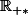
(d'après le théorème de dérivabilité des intégrales à paramètres) avec :
 = \int_0 ^{+ \infty} \frac{\partial f(x,t)}{\partial x} dt)
On vérifie ensuite aisément quepour tout
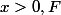
est solution de l'équation différentielle linéaire
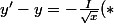)
où
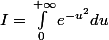
est l'intégrale de Gauss recherchée.
On demande de résoudre cette équation différentielle. On considère
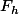
une solution de l'équation homogène associée
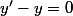
, on trouve facilement
 = Ce^x)
avec

une constante à déterminer.
Pour déterminer une solution particulière de cette équation
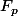
on emploie la méthode de variation de la constante. On considère que
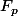
est sous la forme
 = C(x)e^x)
On en déduit
 = C'(x)e^x + C(x) e^x)
et donc, puisque
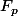
doit être solution de
 : (C'(x)e^x+C(x)e^x) - C(x)e^x = C'(x)e^x= - \frac{I}{\sqrt{x}})
soit finalement
 = - I\frac{e^{-x}}{\sqrt{x}})
Et là on nous sort
 = -I \int_0^{x}\frac{e^{-t}}{\sqrt{t}}dt)
Je ne comprends pas comment on aboutit à ça, enfin je comprends qu'on "passe à l'intégrale" des deux côtés, de sorte qu'on a
 dt = -I\int_0^x \frac{e^{-t}}{\sqrt{t}}dt)
mais comment
 dt)
peut être égal à
)
? Je veux dire
)
ne vaut pas obligatoirement 0 pas vrai ?
Après quoi on rassemble les solution et on dit que
 = F_h(x) + F_p(x) = e^{x}(C - I\int_0^x \frac{e^{-t}}{\sqrt{t}}dt))
ou plutôt
 e^{-x} = (C - I\int_0^x \frac{e^{-t}}{\sqrt{t}}dt))
et, par le changement de variable
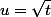
on a que
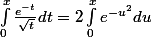
Ainsi
e^{-x} = C-2I\int_0^{x}e^{-u^2}du)
On détermine alors facilement

en

on trouve
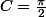
et en faisant tendre

vers

,
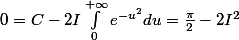
c'est à dire en définitive
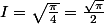
A part le passage de la variation de la constante tout me semble compréhensible, si quelqu'un pouvait m'éclairer sur ce point
D'avance merci
