Exercice avec sigma
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par benjouille93 » 02 Mar 2014, 19:22
par benjouille93 » 02 Mar 2014, 19:22
bonjour,
j'ai besoin d'aide pour un exercice de maths qui dit de calculer An=;)de n=4 à N (1/2)^n
Si je pose Un=(1/2)n, je vois que Un+1=(1/2)*Un
Donc ton calcul est celui d'une somme de termes d'une suite géométrique de raison 1/2. Mais je ne vois pas, comment je peux calculer quelqu'un pourrait me montrer comment faire, s'il vous plait?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 19:27
par barbu23 » 02 Mar 2014, 19:27
Bonjour, :happy3:
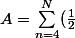^{n} = \displaystyle \sum_{n=0}^{3} ( \frac{1}{2} )^{n} - \displaystyle \sum_{ n =0}^{N} ( \frac{1}{2} )^{n})
Tu finis le calcul. c'est simple.
 par benjouille93 » 02 Mar 2014, 19:31
par benjouille93 » 02 Mar 2014, 19:31
barbu23 a écrit:Bonjour, :happy3:
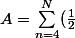^{n} = \displaystyle \sum_{n=0}^{3} ( \frac{1}{2} )^{n} - \displaystyle \sum_{ n =0}^{N} ( \frac{1}{2} )^{n})
Tu finis le calcul. c'est simple.
désolé je vois pas du tout c'est pour ça qu'il me faut au moins un exemple après je retiendrais la méthode mais je vois pas pourquoi vous faite une soustraction?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Mar 2014, 19:39
par barbu23 » 02 Mar 2014, 19:39
Je fais une soustraction pour pouvoir appliquer la formule qui dit que si
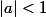
, alors :

. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Mar 2014, 20:16
par Ben314 » 02 Mar 2014, 20:16
Perso, plutôt que d'écrire le truc sous forme d'une soustraction, je préfère factoriser (ça me donne un résultat factorisé à la fin) :
^{n} =\ \sum_{p=0}^{N-4} \Big( \frac{1}{2} \Big)^{p+4} =\ \Big( \frac{1}{2} \Big)^4\ \sum_{p=0}^{N-4} \Big( \frac{1}{2} \Big)^p)
Je t'incite
plus que fortement à faire les deux méthodes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 03 Mar 2014, 15:13
par deltab » 03 Mar 2014, 15:13
Boujour
barbu23 a écrit:Je fais une soustraction pour pouvoir appliquer la formule qui dit que si
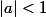
, alors :

. :happy3:
L'égalité que tu as écrite est valable pour
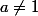
et non pour
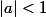
. La condition
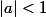
est nécessaire pour la convergence de la suite

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
