Exercice d'analyse

[Anonyme]

Salut!
Voila, j'ai du mal avec l'éxercice suivant, si quelqu'un peu m'aider...

Dans tout l'éxercice, on suppose le réel .
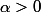
On note la fonction définie par

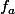
1)Etudier , en distinguant les cas
3)Montrer qu'il existe un réel tel que , pour tout .
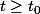
En déduire la convergence de l'intégrale
4)En notant , etablir, par intégration par parties, la relation :


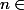
En déduire la valeur de pour tout N*

[fonfon]

salut , je te donne un petit coup de main
1)etude,je te donne la dérivée,aprés c'est une etude normale avec limite...:
f'(t)=e^(-t)[((a-1)t^(a-2)-t^(a-1)]
apres tu etudies les differents cas selon a.

2)Existence:x>0,fixé, t->t^(a-1)e^-t est continue sur [0,x] dc integrable sur [0,x] ( car pdt de fct continues).

3)pour la 1ere partie de la question regarde avec ton etude de fct ça te donneras une idée de ce qu'il faut faire.pour la suite
pour t>=to,on a t^(a-1)e^-t<=e^-t/2
donc integrale de 0 à inf de f(t) <= integrale de 0 a inf de h(t)

avec h(t)=e^-t/2

tu montres que integrale de 0 a inf de h(t) converge (facile) donc l'integrale de f(t) conv.

4) tu remplace par T(a+1) et tu poses u=t^a u'=a*t^(a-1)
v'=e^-t v=-e^-t

apres tu appliques ds la formule de l'IPP uv-intergrale de u'v tu obtiendra le resultat demandé

[Anonyme]

Oki !
Merci beaucoup, je vais voir ça!
Je repasserais surement après !

Merci encore