Exercice d'Analyse L1

[Pilou31]

Bonjour !

A peine arriver en L1 de math/info, je galère deja en analyse.... Je me suis mal orienté, mais j'aime les maths, et la je suis completement bloquer ! Je planche sur un exo d'annale.

Voici le sujet :

1) Resoudre dans C l'equation:

z^7 - 1 = 0

2) Etablir que si z=/=1 ( z different de 1, j'ai pas trouver les notations exactes ) et z solution de l'equation precedente, z verifie z^6 + z^5 + z^4 + z^3 + z² +z +1 = 0

3) Etablir que, si z est solution de l'equation du 1), son conjugé z barre ( notons le Z ) verifie pour k appartient a l'ensemble {O,1,2,3,4,5,6,7}, Z^k = z^(7-k)

4) Deduire des questions precedentes que cos(2pi/7) + cos(4pi/7) + cos (6pi/7) = -1/2

Désolé pour les notations, c'est moche comme ça, mais j'ai pas trouver comment faire mieux.

Alors :

Pour le 1°, j'ai un théorème dans mon cours qui me le fait, et je trouve comme solution les e(i2kpi/7) avec k allant de 0 a 6.

Pour le 2, je seche... Des idées ?

Merci d'avence tout le monde ! ;D

[Luc]

Salut,

1) OK
2) Pense à la somme des 6 premiers termes d'une suite géométrique de raison z et de premier terme 1.
3) Que vaut le module des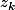 ? Tu vas alors montrer que le conjugué d'un 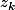est égal à son inverse.
4) c'est un peu plus difficile, pense à la partie réelle dans l'équation de 2)

PS: C'est plutôt de l'algèbre ça! Et de la géométrie. Ce dont on parle n'est rien d'autre que les sommets d'un heptagone régulier de centre O, polygone régulier à 7 côtés.

[Pilou31]

Ok, je reflechit avec ce que tu m'a donné et je te dit si je rebloque ensuite. Par contre le coup de l'heptagone, je te suis pas trop ! Je sors a peine de mon bac moi !

Merci beaucoup en tout cas !

C'est de l'algébre ? je me goure toujours entre les deux ^^

Ps : A si l'eptagone c'est bon je le vois !

[Pilou31]

Bon la 2) ça va, tu m'a casi donner la solution, j'ai juste du chercher la formule. mais effectivement, je la conaissait pas cette formule, du coup c'etait chaux a voir. Enfin bon.

La 3) par contre, je BEUG !

Le module des z(indice k ) c'est 1, vu qu'ils sout la forme e(i2kpi/7).

Ensuite, j'ai passer sous la forme cos + i sin et en factorisant par -i puis en utilisant que cos x = cos (x+pi) je tombe sur conjugé(z(indice k)) = z(indice k) et pas l'inverse.

Je pense m'etre gouré, donc voila ce que j'ai fait : ( z indice k noté z(k) )

z solution de z^7 - 1 = 0 est equivalent a :

Z est sous la forme e(i2kpi/7) avec k de 0 a 7

Donc | z(k) | = 1

=> z(k) = cos ( 2kpi/7 ) + i sin ( 2kpi/7 )

=> conjugé( z(k) ) = cos ( 2kpi/7 ) - i sin ( 2kpi/7 )

=> conjugé( z(k) ) = -i[ cos ( 2kpi/7 - pi/2) +i sin ( 2kpi/7 + pi/2 ) ] ici j'ai juste echangé cos et sin en fesant un quart de tour et en multipliant par -i

=> conjugé( z(k) ) = -i[ cos ( 2kpi/7 + pi/2) +i sin ( 2kpi/7 + pi/2 ) ] car cosinus est paire

=> conjugé( z(k) ) = -i z(k) e(-ipi/2)

=> conjugé( z(k) ) = -i z(k) i = z(k).

je trouve pas l'erreur...

[Luc]

=> z(k) = cos ( 2kpi/7 ) + i sin ( 2kpi/7 )

=> conjugé( z(k) ) = cos ( 2kpi/7 ) - i sin ( 2kpi/7 )

On peut s'arrêter là, cette formule suffit pour conclure. Que penses-tu de exp(-2ikpi/7) ?

[Pilou31]

Bon, je me repond a moitié moi meme, mais je vient de me rendre compte que c'est pas cos x = cos ( x+pi ) c'etait gros comme bourde.

Du coup j'ai cette erreur en moin, mais je suis toujour coincé. Dsl pour le multi post, quand j'aretterais de reflechir je metrait tout dans le meme post, et je ferais qqch de plus lisisble. Mais la je met mes reflexions au fur et a mesure un peu.

[Pilou31]

J'avais pas vu ton message...

Bon, j'ai trouver une formule dans mon cours qui corespond un peu plus a ce que tu m'a dit :

|z(k)| = 1

Donc z(k) * conjugé(z(k)) = 1² = 1 donc il est l'inverse de son conjugé.

Mais ça me donne du conjugé(z(k)^k = z(k)^(-k) et pas z(k)^(7-k) comme le demande l'énoncé.

Ma reponce a ton post :

Le moins peut sortir de l'exp, non ? Exp(-2ikpi/7) = -exp(2ikpi/7 )

Mais je n'arive pas a faire le lien logique entre
conjugé( z(k) ) = cos ( 2kpi/7 ) - i sin ( 2kpi/7 )
et
Exp(-2ikpi/7) = -exp(2ikpi/7 )
et ce qu'on me demande d'etablir, a savoir
conjugé(z(k))^k = z(k)^(7-k)

je me suis fait un dessin, mais ça m'a pas aider XD

PS :

J'edite au lieu de faire encore un post.

Je trouve bien de manière pas trop afreuse que le conjugé des Zk est egal a leur inverse. Sauf qu'on me demande de montrer qu'ils sont egals a z^(7-k) et la j'ai z^(-k).

En fait, en ecrivant ça j'ai trouver, faut juste multiplier par 1 d'un coté, et par z^7 de l'autre, qui est bien l'equation du tout debut...

Comme quoi a force de tourner en rond, on finit par trouver !

Bon, je redige ça, je planche sur la question suivante, et je revient vous dire comment ça ce passe.

[Luc]

J'avais pas vu ton message...

Bon, j'ai trouver une formule dans mon cours qui corespond un peu plus a ce que tu m'a dit :

|z(k)| = 1

Donc z(k) * conjugé(z(k)) = 1² = 1 donc il est l'inverse de son conjugé.

Exactement!

Mais ça me donne du conjugé(z(k)^k = z(k)^(-k) et pas z(k)^(7-k) comme le demande l'énoncé.

Oui mais que vaut z(k)^7?

Le moins peut sortir de l'exp, non ? Exp(-2ikpi/7) = -exp(2ikpi/7 )

Ça par contre on a pas le droit :zen: . Sinon on aurait des trucs absurdes du genre 0=1...

Tu y es presque!
Sur un dessin, le fait de conjuguer c'est faire la symétrie par rapport à l'axe des abscisses.

[Pilou31]

HAHA, tu post pile au moment ou j'edite !

Du coup, j'ai trouver seul en ecrivant que je trouvais pas XD

Bon, je regarde la suite.

Edit : Ben j'ai chercher la partie reelle... mais la partie relle d'une somme c'ets la some des partie reelles, par contre pour le produit ça marche pas vraiment...

Et moi j'ai des z^6 qui ce balade joyeusement :ptdr: !

Edit 2 : ça sent l'astuce, mais je la trouve pas. je vais pisser, pis j'essaye en partant des Cos pour essayer d'ariver a l'equation du 2) ( dans l'autre sens quoi, ce serra peut-etre plus evident ! )

Edit 3 : Bon, Les cosinus corespondent bien aux parties reelles, mais après je trouve toujour pas comment les combiné pour avec qqch qui corespond... Ça commence a bien me casser la tete XD
Surtout que derière j'ai un autre exo !

Edit 4 : EUREKA ! Tout corps plongé dans l'eau ressort mouillé ! Euh on, je m'egare ^^

Non enfait, falais juste combiné la reponce a la question 2 avec celle a la question 3, du coup j'ai avencer un peu.

J'ai remplacer les z^6 5 et 4 par z^ 7-1, 7-2, et 7-3, puis trasformé en conjugé(z)^1,2,3.

Du coup, je me retrouve avec ça :

2Re(z) + z^2 + conj(z)^2 + z^3 + conj(z)^3 +1 = 0

J'y suis presque !

Du coup ma question est la suivante : Est-ce que le caré du conjugé c'est le conjugé du carré ? ( et pour le cube, et les puissances en general enfait... )

Au passage, j'etait trop a fond, j'ai meme pas penser a le dire, mais merci beaucoup pour ton aide ! Franchement, c'est agreable de voir qu'il y a encore des gens pret a aider leur prochains :)

[Pilou31]

Bon, ben finalement, j'ai developper :

2Re(z) + z^2 + conj(z)^2 + z^3 + conj(z)^3 +1 = 0

<=> 2x^3 + 2x^2 + 2y^2 - 6xy^2 = -1 avec z=x+iy

Je vais te me transformer tout ça en cossinus/sinus et te me linéarisé tout ça moi ! J'ai pas trouver l'astuce, alors je bourine :P

[Pilou31]

Je trouve des coeficients degeu sur mes cosinus a la fin... Mais par contre j'ai Zero sinus une fois la linearisation finie !

Mais bon au lieux de (1,1,1) comme coef, j'ai du (1,7,3). Bonjours les erreurs de calcul...

J'estime avoir bien travailler pour ce soir ! STOP ! XD

[Luc]

Ben j'ai chercher la partie reelle... mais la partie relle d'une somme c'ets la some des partie reelles, par contre pour le produit ça marche pas vraiment...

On récapitule : tu es tombé sur l'équation
En passant à la partie réelle, tu as
Effectivement n'est pas égal à . En revanche, on a le droit de dire que . Cela résulte de la formule de de Moivre : .
Maintenant, il faut utiliser deux choses :
- le résultat de la question 3) : pour k appartient a l'ensemble {O,1,2,3,4,5,6,7}, Z^k = z^(7-k). Du coup le conjugué de z c'est z^6, le conjugué de z^2 c'est z^5, le conjugué de z^3 c'est z^4. Cela se voit bien sur le dessin : l'heptagone est symétrique par rapport à l'axe des abscisses, donc la symétrie par rapport à cet axe envoie un sommet sur un autre sommet.
- le fait que deux nombres complexes conjugués ont la même partie réelle.

Bonus: tu peux interpréter le résultat de la question 4 comme l'abscisse d'un barycentre de trois sommets qui vaut -1/2.

[Pilou31]

Merci beaucoup beaucoup beaucoup !!! J'ai pu enfin en finir ;)

Tu m'a été d'une grande aide, je te remercie beaucoup. C'est très simpa comme concept d'entraide :)

[Luc]

Merci beaucoup beaucoup beaucoup !!! J'ai pu enfin en finir

Tu m'a été d'une grande aide, je te remercie beaucoup. C'est très simpa comme concept d'entraide

Tant mieux :we: