Espaces metriques !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 09:53
par barbu23 » 12 Déc 2007, 09:53
Bonjour :
On vient de terminer les espaces topologiques il y'a quelques jours .. on est maintenant dans les espaces metriques, et j'ai encore rien reviser à ce sujet là sauf quelques rudiments des années passés que je connais !
Alors, voiçi ma question :
 $)
un espace metrique .
 = \inf \{ 1 , d(x,y) \} $)
 = \frac{d(x,y)}{1 + d(x,y) \} $)
Alors, je voudrai savoir pourquoi

et

et

sont topologiquement équivalentes et pourquoi

et

sont comparables, mais

et

ne sont pas en general comparables ?
Merci infiniment !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 09:57
par barbu23 » 12 Déc 2007, 09:57
Pour

et

qui ne sont pas en general comparables, c'est parceque si on se place dans
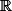
par exemple, et on met :
 = |x-y| $)
et
 = \inf \{ 1 , |x-y| \} $)
, alors

est non bornée et

est bornée par

.. donc, il ne sont pas comparables .

et

sont comparables, parceque si :
 \geq 1 $)
, alors :
 $)
et
 = 1 \leq 2 . \frac{d(x,y)}{1+d(x,y)} = \frac{d(x,y)+d(x,y)}{1+d(x,y)} = 2.d_{2}(x,y) $)
, donc, ils sont comparables !
Si, maintenant,
 \leq 1 $)
, alors :
 = d(x,y) \geq \frac{d(x,y)}{1+d(x,y)} = d_{2}(x,y) $)
, on a également :
 = \frac{d(x,y)}{1+1} \leq \frac{d(x,y)}{1+d(x,y)} = d_{2}(x,y) $)
.. donc, ils sont comparables !
maintenant, il reste à montrer qu'ils sont topologiqument equivalentes !
Merci d'avance de votre aide !
 par legeniedesalpages » 12 Déc 2007, 10:15
par legeniedesalpages » 12 Déc 2007, 10:15
barbu23 a écrit:Pour

et

qui ne sont pas en general comparables, c'est parceque si on se place dans
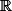
par exemple, et on met :
 = |x-y| $)
et
 = \inf \{ 1 , |x-y| \} $)
, alors

est non bornée et

est bornée par

.. donc, il ne sont pas comparables .

et

sont comparables, parceque si :
 \geq 1 $)
, alors :
 $)
et
 = 1 \leq 2 . \frac{d(x,y)}{1+d(x,y)} = \frac{d(x,y)+d(x,y)}{1+d(x,y)} = 2.d_{2}(x,y) $)
, donc, ils sont comparables !
je pense que c'est àa, pour ton contre-exemple, tu peux prendre x=0, y=n
et tu aboutis à
 = |n| $)
et
 = \inf \{ 1 , |n| \} $)
et il est clair qu'on peut pas les comparer.
 par legeniedesalpages » 12 Déc 2007, 10:21
par legeniedesalpages » 12 Déc 2007, 10:21

et

sont comparables, donc topologiquement équivalente,
après pour les autres peut être en montrant que les applications
\rightarrow (E,d))
et
\rightarrow (E,d))
sont des homéomorphismes.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:23
par barbu23 » 12 Déc 2007, 10:23
oui voilà ! et pour "topologiquement comparables" ?
Pour

et

, il faut montrer que

, c'est à dire "que la topologie de

engendré par les boules
 $)
est la même que celle engendré par les boules
 $)
, c'est ça ? on prend un ouvert
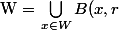 $)
et on montre que
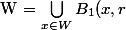 $)
et vice versa !! c'est ça ? n'est ce pas ?
 par legeniedesalpages » 12 Déc 2007, 10:28
par legeniedesalpages » 12 Déc 2007, 10:28
je crois qu'il y a même pas besoin vu que les boules ouverts forment une base, il suffit que tu montres qu'une boule ouverte pour

est ouverte pour

et qu'une boule ouverte pour

est ouverte pour

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:36
par barbu23 » 12 Déc 2007, 10:36
Et là c'est facile à faire : on a :
 \subset B_{1}(x,\alpha .r) $)
avec

( qui depend de la boule, parceque

n'est pas bornée ) et
 \subset B(x,r) $)
, parcequ'il sont comparables ... pour les autres metriques, c'est evident, parceq'ils sont comparables !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:38
par barbu23 » 12 Déc 2007, 10:38
legeniedesalpages a écrit:je crois qu'il y a même pas besoin vu que les boules ouverts forment une base, il suffit que tu montres qu'une boule ouverte pour

est ouverte pour

et qu'une boule ouverte pour

est ouverte pour

.
Oui, voilà !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:40
par barbu23 » 12 Déc 2007, 10:40
J'ai une autre question à vous poser :
Pourquoi : si

muni de la topologie

, alors

n'est pas metrisable ?
Merci d'avance de votre aide !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:45
par barbu23 » 12 Déc 2007, 10:45
Il faut montrer qu'il n'existe pas de distances

telle que :

, c'est ça ?
Parceque , un espace topologique

est dit metrisable s'il existe une distance

sur

telle que

soit la topologie de

, et la topologie de

c'est quoi ? c'est

, n'est pas ? donc, il faut montrer qu'il n'existe pas de

telle que

... !
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 12 Déc 2007, 10:47
par BQss » 12 Déc 2007, 10:47
barbu23 a écrit:J'ai une autre question à vous poser :
Pourquoi : si

muni de la topologie

, alors

n'est pas metrisable ?
Merci d'avance de votre aide !!
Si E était metrisable sous cette topologie il existerait pour toute paire d'élements distinctes, deux ouverts distinctes les contenants car un espace métrique est séparable, ce qui n'est pas le cas avec la topologie

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2007, 10:56
par barbu23 » 12 Déc 2007, 10:56
oui, voilà, ça aussi !
il suffit de remarquer aussi, que : pour une distance quelconque ( quelque soit )

,
 = \{ 1 \} \in \mathcal{T}_{d} \not \in \mathcal{T} $)
, avec
 , d(1,3) , d(2,3) \} $)
par exemple !
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 12 Déc 2007, 10:57
par BQss » 12 Déc 2007, 10:57
Et métrisable ca veut juste dire qu'il existe une distance définissant les ouverts de la topologie. Ici il n'y en a donc aucune capable de le faire...
 par legeniedesalpages » 12 Déc 2007, 11:07
par legeniedesalpages » 12 Déc 2007, 11:07
oui pour regarder si une topologie est non métrisable, on regarde d'abord si elle est séparée ou non, et si elle est ben on pousse un peu plus les recherches.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2007, 15:58
par barbu23 » 15 Déc 2007, 15:58
Bonjour :
Est ce que dans un fermé d'un espace métrique quelconque, toute suite de ce fermé est convergente ?
Merci infiniment !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2007, 16:02
par barbu23 » 15 Déc 2007, 16:02
D'accord ! pas necessairement vrai ! parceque pour
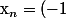^{n} $)
, elle est contenue dans

qui est fermé dans
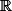
, mais la suite ne converge pas ! :lol2:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Déc 2007, 16:02
par ThSQ » 15 Déc 2007, 16:02
Forcément que non vu que l'espace lui-même est un fermé.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 15 Déc 2007, 16:03
par Joker62 » 15 Déc 2007, 16:03
La caractérisation séquencielle des fermés :
Soit A une partie fermée de (E,d)
A est fermé <=> Pour toute suite convergente de A, on a que la limite reste dans A
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2007, 16:09
par barbu23 » 15 Déc 2007, 16:09
oui, c'est exactement ça auquel je pensais !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2007, 20:49
par barbu23 » 15 Déc 2007, 20:49
Bonsoir :
Un espace vectoriel localement compact est de dimension finie, donc la boule unité est compact ! j'aimerai savoir pourquoi dans ce cas là, toute boule fermé est compact ?
Merci d'avance !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
