Bonjour
Un exercice demande de démontrer qu' une famille constituée d une fonction polynôme P de degré n et ses n fonctions dérivées successives est linéairement indépendante.
La démonstration est-elle valide en faisant une récurrence sur n, amorcée avec n = 0?
Merci de me dire
Espace vectoriel des fonctions polynôme
11 messages
- Page 1 sur 1
J'ai un doute sur le point suivant
Corps de la récurrence (2ème étape) :
On suppose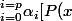]^i = 0 \Longrightarrow (\alpha_0;\alpha_1;.....;\alpha_p) = (0;0;.........;0))
Hérédité (3ème étape)
Si le corps de la récurrence est supposé vrai, alors
]^i = 0 \Longleftrightarrow \Bigsum_{i=0}^{i=p}\alpha_i [P(x)]^i + \alpha_{p+1}[P(x)]^{p+1}= 0)
et dans ces conditions on peut/pourrait écrire]^{p+1}= -\Bigsum_{i=0}^{i=p}\alpha_i [P(x)]^i) , en tout cas çane me semble pas nécessairement incompatible avec l'hypothèse précédente, ou bien ? auquel cas la famille des p+2 polynômes serait liée.
, en tout cas çane me semble pas nécessairement incompatible avec l'hypothèse précédente, ou bien ? auquel cas la famille des p+2 polynômes serait liée.
Donc mon doute porte sur la façon de passer de la 2ème étape qui n'entraînerait pas NECESSAIREMENT la 3ème.
Merci de me dire ce que vous en pensez
>>Zygomatique : que dois-je comprendre par "résultat sur les degrés"?
Corps de la récurrence (2ème étape) :
On suppose
Hérédité (3ème étape)
Si le corps de la récurrence est supposé vrai, alors
et dans ces conditions on peut/pourrait écrire
Donc mon doute porte sur la façon de passer de la 2ème étape qui n'entraînerait pas NECESSAIREMENT la 3ème.
Merci de me dire ce que vous en pensez
>>Zygomatique : que dois-je comprendre par "résultat sur les degrés"?
>>Mikihisa : je n'ai pas bien saisi ton idée ; si je te suis bien, je devrais former une matrice triangulaire (n+1;n+1) aux coefficients parfois assez longs à écrire... et ensuite ? L'exercice étant donné dans le cadre d'un chapitre situé avant l'étude des matrices, je ne pense pas que ce soit la méthode attendue, mais pourquoi pas ?
Peut-être ton idée d'écrire une matrice pourrait-elle se ramener à poser un système de n+1 équations homogènes à n+1 inconnues au total, non ?
Merci de me dire
Peut-être ton idée d'écrire une matrice pourrait-elle se ramener à poser un système de n+1 équations homogènes à n+1 inconnues au total, non ?
Merci de me dire
:doh:
soit P un polynome de degré n ...
soit a_0, a_1, ..., a_n des réels tels que} = 0) (1)
(1)
le monome de plus haut degré n appartient à P donc (1) est vraie implique que a_0 = 0
on recommence avec P' .... et le seul monome de degré n - 1 ....
soit P un polynome de degré n ...
soit a_0, a_1, ..., a_n des réels tels que
le monome de plus haut degré n appartient à P donc (1) est vraie implique que a_0 = 0
on recommence avec P' .... et le seul monome de degré n - 1 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Si je t'ai bien compris,
à partir de la définition du polynôme nul qui stipule que c'est le polynôme dont tous les coefficients sont nuls, en développant (1) on ne trouve qu'un unique terme (monôme) de degré n, dont le coefficient est le produit du coefficient non nul du terme de degré n dans P multiplié par , donc nécessairement
, donc nécessairement  est nul.
est nul.
Sachant que est nul, on poursuit avec le terme de degré n-1 dans (1) développé, et on déduit rapidement que
est nul, on poursuit avec le terme de degré n-1 dans (1) développé, et on déduit rapidement que  est nul et de proche en proche en proche que tous les
est nul et de proche en proche en proche que tous les  sont nuls.
sont nuls.
merci
à partir de la définition du polynôme nul qui stipule que c'est le polynôme dont tous les coefficients sont nuls, en développant (1) on ne trouve qu'un unique terme (monôme) de degré n, dont le coefficient est le produit du coefficient non nul du terme de degré n dans P multiplié par
Sachant que
merci
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
