Espace ultra-métrique

par **legeniedesalpages** » 02 Nov 2007, 12:56

Bonjour je bloque sur cet exercice;

Soit

un espace ultra-métrique,

ie

est un espace métrique vérifiant de plus l'inégalité ultra-triangulaire :

pour tous

.

Montrer que, pour cette distance, deux boules sont soit disjointes, soit confondues.

Merci pour votre aide.

par **tize** » 02 Nov 2007, 13:25

Bonjour,
par confondues tu veux dire que l'une est incluse dans l'autre ?

par **ThSQ** » 02 Nov 2007, 14:04

avec

Soit

alors

Donc

!

Pareil pour les boules fermées.

par **tize** » 02 Nov 2007, 14:07

Bonjour ThSQ...

par **ThSQ** » 02 Nov 2007, 14:16

tize a écrit:Bonjour ThSQ...

Bonjour Tize

Est-ce une message submiminal pour insinuer que j'ai manqué de politesse ici ...
Bon, je m'en excuse. Me pardoneras-tu pour cette fois ?

par **Lierre Aeripz** » 02 Nov 2007, 14:18

Les distances ultramétriques sont vraiment étranges.

Voici quelques résultats :

Si , alors
et

NB : S est la sphère, B la boule ouverte, et

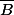
la boule fermée.

par **tize** » 02 Nov 2007, 14:22

Non, non, aucun souci ThSQ :we:
Merci pour toutes ces précisions Lierre Aeripz.

par **ThSQ** » 02 Nov 2007, 15:27

tize a écrit:Non, non, aucun souci ThSQ

Bon, OK .... Comprô rien mais pô grave.

Parmi les multiples bizarreries du zoo ultramétrique, j'aime bien celle-ci :

Dans un Banach ultramétrique une série converge ssi son terme général tend vers zéro !

par **tize** » 02 Nov 2007, 15:56

ThSQ a écrit:...
Parmi les multiples bizarreries du zoo ultramétrique, j'aime bien celle-ci :
Dans un Banach ultramétrique une série converge ssi son terme général tend vers zéro !

Aha...intéressant, je ne connaissais pas, effectivement bizarre...

par **legeniedesalpages** » 02 Nov 2007, 16:13

Merci pour vos réponses, déjà pour celles de ThSQ:

ThSQ a écrit:

avec

Soit
alors

Donc !

Pareil pour les boules fermées.

Je suis bien d'accord, mais ça ne montre pas qu'elles sont confondues, il faut encore montrer qu'on a

, et là je ne vois pas vraiment comment procéder.

par **legeniedesalpages** » 02 Nov 2007, 16:20

Apparemment, vu un des résultats étrange de Lierre Aeripz, il suffit que je montre que

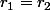
, je vais creuser ça.

par **ThSQ** » 02 Nov 2007, 17:01

Bon courage pour montrer ça car c'est faux bien sûr (sauf dans un espace réduit à un élément :ptdr: )

par **legeniedesalpages** » 02 Nov 2007, 17:04

D'accord, je veux bien le croire, as-tu un un contre-exemple (ça pourrait ainsi faire aussi office d'exemple d'espace ultra-métrique)?

par **ThSQ** » 02 Nov 2007, 17:13

Q muni de la "valeur absolue" p-adique par exemple

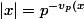avec

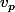
= valuation p-adique = exposant de p dans la décomposition de x.

Pour revenir à ton pb d'origine. Si deux boules ayant un point en commun étaient égales, toutes les boules de même centre seraient égales ! Et l'espace ne serait même pas séparé ce qui fait désordre pour un métrique.

par **legeniedesalpages** » 02 Nov 2007, 17:15

ah oui effectivement,

un exemple + la non-séparation d'un espace métrique = pas possible.

Effectivement je n'y avais pas pensé.

Merci ThSQ.

Espace ultra-métrique

espace ultra-métrique

Qui est en ligne