Espace compact

par **Ben314** » 10 Nov 2010, 22:27

Oui, c'est correct.
Pour la dernière question, j'ai pas trop réfléchi pour trouver quelque chose de "subtil", donc à la bourrin : tu raisonne par l'absurde, tu considère le complémentaire de f(L) et tu n'oublie pas que F est supposé localement compact...

par **barbu23** » 10 Nov 2010, 23:09

Ben314 a écrit:tu raisonne par l'absurde, tu considère le complémentaire de f(L) et tu n'oublie pas que F est supposé localement compact...

Par absurde, supposons que

n'est pas fermé, il faut arriver à montrer que

n'est pas fermé, ce qui est en contradiction avec le resultat de la question precedente ! mais je sèche encore sur cette question.

par **barbu23** » 11 Nov 2010, 10:39

un peu d'aide svp :happy3:

par **Ben314** » 11 Nov 2010, 11:40

En fait, en relisant l'énoncé, pour montrer que

est pas fermé, ben y'a aucun calcul à faire :

On est parti d'un

, on a montré que

(pour un certain

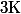
) puis que

est fermé. On a donc

et en particulier

...

par **barbu23** » 11 Nov 2010, 11:45

Ben314 a écrit:En fait, en relisant l'énoncé, pour montrer que est pas fermé, ben y'a aucun calcul à faire :

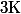
On est parti d'un , on a montré que (pour un certain ) puis que est fermé. On a donc et en particulier ...

donc,

et par conséquent :

MErci beaucoup Ben314 :happy3:

Espace compact

Qui est en ligne