Espace des fonctions continues à support compact

[foufa2]

Bonjour,

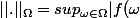je veux determiner la fermeture de (l'espace des fonctions continues à support compact) dans (),où est l'espace des fonctions continues borne et . Sachant que est une espace topologique separée.

Qui a une reponse? je pense que , mais j'en suis pas sure.

[Ben314]

Salut,
Tu as pas un tout petit peu l'impression que ça va dépendre de ton truc ?
- Par exemple, si est lui même un espace topologique compact, c'est quoi ? et ?
- Si c'est un ensemble (infini) muni de la topologie discrète, c'est quoi dans ce cas ? et ?

[foufa2]

T'as raison Ben, dans mon cas, est une espace topologique separée

[Ben314]

C'est (très loin) d'être suffisant pour conclure : dans les deux exemples que je te donne, l'espace Omega est séparé or les conclusions ne sont pas du tout les mêmes.
Tu trouve quoi pour le premier exemple ? Et pour le deuxième ? (et c'est quoi dans les deux cas l'adhérence de CK(Omega) dans Cb(Omega) ?)

Sinon, si ça t'intéresse (et en supposant au départ Omega séparé), en fait il y a équivalence entre
(i)
(ii) est compact
(iii)

Pourquoi ?

[arnaud32]

je dirais plutôt que

[foufa2]

Salut ben,
il est facile de voir que et par suite , Mais comment peux je monter que ?(il suffit de montrer que est un ferme)?

[Ben314]

Salut ben,
il est facile de voir que ...

Ça m'intéresserait fortement que tu m'explique comment tu voit "facilement" une telle inclusion...

[foufa2]

c`est facile a voir bien sur dans le cas ou notre espace est un espace compact.
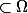
En effet, soit alors supp(f) et il est fermé est par suite le support de la fonction f est un compact. et donc

[Ben314]

c`est facile a voir bien sur dans le cas ou notre espace est un espace compact.

Et c'était écrit où dans ton précédent post que tu supposait compact ?

...et par suite , Mais comment peux je monter que ?

Je te rappelle que l'énoncé précise bien que tu cherche l'adhérence de dans .
Et l'adhérence de X dans X, ben c'est trivialement ...

[foufa2]

oui, Merci beaucoup.
J` ai une autre question. Dans le cas ou est relative compact, l'adhérence de est-il aussi ?

[Ben314]

Dans le cas ou est relative compact...

C'est quoi un "espace relative compact" ?
(perso, tout ce que je connait, c'est la notion de partie relativement compacte)

[foufa2]

dsl , mais je voulais dire localement compacte.