Espace compact
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 13:52
par barbu23 » 09 Nov 2010, 13:52
Soit

un espace toplogique séparé,

un espace localement compact et

une application continue.
On dit que

est propre si pour tout compact

de

 $)
est un compact de

- Montrerq ue si

est compact alors

est propre
Donner un exemple d'applications :

continue, mais non propre.
Soit

un sous espace fermé de

, montrer que l'application

definie par :
 = x $)
est propre.
On suppose que

ets propre.
Soit

un fermé de

, on veut montrer que
 $)
est un fermé de

Soit
} $)
et

un voisiange compact de

dans

Montrer que
} $)
Montrer que
 = f(f^{-1}(K) \bigcap L ) $)
En dedurie que
 $)
est fermé.
En deduire que
 $)
est fermé.
Merci d'avance.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Nov 2010, 13:57
par Nightmare » 09 Nov 2010, 13:57
Salut,
qu'est-ce que tu n'arrives pas à faire?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 14:08
par barbu23 » 09 Nov 2010, 14:08
Alors, pour la première question, il s'agit de montrer que

est propre.
Soit

un compact de

localement compact, donc séparé, par conséquent

est fermé et donc
 $)
est fermé car

est continue. Par hypothèse

est compact, donc :
 $)
est compact
Je n'arrive pas à resoudre la deuxième question.

:mur:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 14:16
par barbu23 » 09 Nov 2010, 14:16
Pour la seconde question :
On prend :
 $)
qui est continue et

qui est un fermé bornée de

, donc compact, et
 = \{ n \pi \}_{n \geq 0} $)
n'est pas bornée ( divergente ), donc n'est pas compact.
Par conséquent :

est non propre.
Pour la question suivante, qu'estce qu'on fait ? :happy3:
MErci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Nov 2010, 14:20
par Ben314 » 09 Nov 2010, 14:20
Salut,
barbu23 a écrit:...Montrer que
 = \overline{f^{-1}(l) \bigcap L })
...
ça ne serait pas plutôt
 = f\left(f^{-1}(K) \cap L\right))
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 14:23
par barbu23 » 09 Nov 2010, 14:23
Ben314 a écrit:Salut,ça ne serait pas plutôt
 = f\left(f^{-1}(K) \cap L\right))
?
Oui, voilà, j'ai trop vite écrit Ben :happy3:
MErci pour la correction :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 16:54
par barbu23 » 09 Nov 2010, 16:54
Un peu d'aide svp :happy3:
Merci d'avance. :happy3:
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 09 Nov 2010, 19:12
par windows7 » 09 Nov 2010, 19:12
ah j'ai eu ca au partiel hier, ok s'en tape dma vie :)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Nov 2010, 19:52
par Ben314 » 09 Nov 2010, 19:52
Si tu en est là :
barbu23 a écrit:Soit

un sous espace fermé de

, montrer que l'application

definie par :

est propre.
ben il suffit décrire la définition de "propre" !!!
Si tu en est là :
barbu23 a écrit:Montrer que

je vois qu'une seule méthode : revenir à la définition de l'adhérence d'une partie.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 20:36
par barbu23 » 09 Nov 2010, 20:36
Ben314 a écrit:Si tu en est là : ben il suffit décrire la définition de "propre" !!!
Si tu en est là : je vois qu'une seule méthode : revenir à la définition de l'adhérence d'une partie.
Soit

un compact de

donc, fermé de

, car

est localement compact.
Alors
 = H \bigcap K $)
est fermé de

contenue dans

qui est compact, donc
 $)
est compact
CQFD

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Nov 2010, 20:42
par Ben314 » 09 Nov 2010, 20:42
Vu que K est contenu dans F, tu peut même directement écrire que
 = K)
!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 20:51
par barbu23 » 09 Nov 2010, 20:51
Soit
 } $)
Alors
 $)
:
 \neq \emptyset $)
Par hypothèse,

est un voisinage compact de

dans

.
alors,

un ouvert de

tel que

 $)
car
 $)
et donc

ouvert de

tel que

Par conséquent :

avec

un ouvert de

.
Par conséquent
 $)
.
et il est clair que
 \neq \emptyset $)
car :
} $)
Merci pour votre aide. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Nov 2010, 20:59
par Ben314 » 09 Nov 2010, 20:59
barbu23 a écrit:...il faut trouver
 $)
tel que
 \neq \emptyset $)
...
non, pour montrer que
} $)
, il ne faut pas
"
trouver un  $)
tel que..."
mais montrer que,
"
pour tout  $)
on a
 \neq \emptyset $)
"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Nov 2010, 21:03
par barbu23 » 09 Nov 2010, 21:03
barbu23 a écrit:Soit
 } $)
Alors
 $)
:
 \neq \emptyset $)
Par hypothèse,

est un voisinage compact de

dans

.
alors,

un ouvert de

tel que

 $)
car
 $)
et donc

ouvert de

tel que

Par conséquent :

avec

un ouvert de

.
Par conséquent
 $)
.
et il est clair que
 \neq \emptyset $)
car :
} $)
Merci pour votre aide. :happy3:
c'est correct la suite Ben241 ? :help:
Merci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Nov 2010, 00:39
par Ben314 » 10 Nov 2010, 00:39
Oui, c'est parfaitement correct, mais il n'est pas utile de prendre à chaque fois des ouverts contenus dans les voisinages : tu peut directement prendre l'intersection de tes deux voisinages K et A de y, ce sera aussi un voisinage de y donc il rencontrera f(L) vu que y est dans l'adhérente de f(L).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2010, 20:35
par barbu23 » 10 Nov 2010, 20:35
Merci Ben314 : happy3:
Maintenant comment établir la formule suivante :
 = f(f^{-1}(K) \bigcap L) $)
J'ai pensé faire comme ça ( mais mène à rien ) :
 = f(f^{-1}(K \bigcap f(L))) = f(f^{-1}(K) \bigcap f^{-1}(f(L))) \neq f(f^{-1}(K) \bigcap L) $)
As tu une piste Ben314 ? :happy3:
MErci d'avance :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Nov 2010, 21:00
par Ben314 » 10 Nov 2010, 21:00
Ben "ma piste" (si on peut parler de piste...) , c'est, pour un
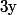
donné de

,
- Quoi ça veut dire que
)
?
- Quoi ça veut dire que
 \cap L))
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2010, 21:33
par barbu23 » 10 Nov 2010, 21:33
Ben314 a écrit:Ben "ma piste" (si on peut parler de piste...) , c'est, pour un
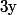
donné de

,
- Quoi ça veut dire que
)
?
- Quoi ça veut dire que
 \cap L))
?
si :
 \cap L) $)
alors :
 \cap L $)
tel que
 $)
donc :
 $)
et

c'est àdire :
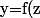 \in K $)
et
 \in f(L) $)
Par conséquent :
 $)
c'est à dire :
 \cap L) \subset K \bigcap f(L) $)
Montrons maintenant que :
 \subset f(f^{-1}(K) \cap L) $)
Si
 $)
alors

et
 $)
c'est à dire :

tel que
 $)
et
 $)
donc
 \bigcap L $)
et donc
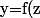 \in f(f^{-1}(K) \bigcap L) $)
Par conséquent :
 \subset f(f^{-1}(K) \cap L) $)
CQFD. :happy3:
C'est correct Ben314 ??? :happy3:
Maintenant, comment deduire que
 $)
est fermé ?
Celà revient à montrer que
 \bigcap L) $)
est fermé. pourquoi ce dernier est fermé ?
MErci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Nov 2010, 21:40
par Ben314 » 10 Nov 2010, 21:40
Oui, c'est correct.
Pour la fin, cherche un peu : c'est trés simple (et n'oublie pas que f est supposée propre)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2010, 21:54
par barbu23 » 10 Nov 2010, 21:54
Ben314 a écrit:Oui, c'est correct.
Pour la fin, cherche un peu : c'est trés simple (et n'oublie pas que f est supposée propre)
Alors

st compact et

est propre donc
 $)
est compact dans

separé, donc
 $)
est fermé et

est fermé donc
 \bigcap L $)
est fermé dans le compact
 $)
, donc
 \bigcap L $)
est compact et

par hypothèse est continue, donc
 \bigcap L) $)
est compact dans

séparé, car localement compact, donc
 \bigcap L) $)
est fermé et par suite
 $)
est fermé.
C'est bien comme ça Ben314 ??? :happy3:
Maintenant, pour la dernière question, pourquoi
 $)
est fermé ??? :mur:

là, jene vois pas du tout comment m'y prendre pour cette question.
Merci d'avance. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
un sous espace fermé de
, montrer que l'application
definie par :
est propre.
:
est un voisinage compact de
dans
.
un ouvert de
tel que

car
et donc
ouvert de
tel que
avec
un ouvert de
.
.
car :
donné de
,
?
?