Erreur quadratique moyenne / Espérance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 20 Jan 2019, 17:23
par fioldodidi » 20 Jan 2019, 17:23
Bonjour,
Je suis bloqué dans un calcul d’espérance, on a :
Sujet : 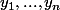
~
)
et
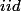
Estimateur :
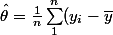^2)
avec
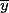
moyenne empirique de

qui estime
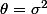 Question :
Question :Erreur quadratique moyenne :
 = E[\mid\mid \hat{\theta} - \theta\mid\mid^2]) Ma réponse :
Ma réponse :  = E[\mid\mid \hat{\theta} -\theta\mid\mid^2] = E[\mid\mid\frac{1}{n} \sum_1^n (y_i)^2-\sigma^2\mid\mid^2])
Mais je ne vois pas comment faire rentrer l’espérance ou avancer, une idée

?
Merci !
-
cassiopella
- Membre Naturel
- Messages: 50
- Enregistré le: 20 Jan 2019, 14:47
-
 par cassiopella » 20 Jan 2019, 20:04
par cassiopella » 20 Jan 2019, 20:04
Dans le cours vous avez du voir comment l'expression de l'erreur quadratique moyenne peut être transformée : biais de l'estimateur plus variance de l'estimateur :
https://fr.wikipedia.org/wiki/Erreur_quadratique_moyenne#ExpressionIl faut donc trouver le biais et la variance de l'estimateur. Pour te faciliter la vie, je te suggère de simplifier un peu l’expression de la variance empirique.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 11:22
par fioldodidi » 22 Jan 2019, 11:22
Merci,
^2] = E[(y_1-\bar{y} )^2] = \sigma - 2\bar{y} E[y_1] = \sigma)
donc
 = 0)
et
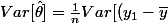^2] = \frac{1}{n} Var[(y_1 )^2] - 4\bar{y}\sigma^2)
Je suis bloqué sur l'expression de la variance, quelqu'un trouverai pas une erreur par hazard

?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 22 Jan 2019, 14:07
par Sylviel » 22 Jan 2019, 14:07
Bonjour,
ça me semble bourré d'erreurs ^^
pour commencer il faut développer proprement le carré, et ensuite se souvenir que l'espérance du carré d'une variable centrée c'est la variance, pas l'écart-type

Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Jan 2019, 14:21
par Lostounet » 22 Jan 2019, 14:21
Tu essayes de faire quoi au juste?
Une décomposition biais-variance on dirait...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 15:02
par fioldodidi » 22 Jan 2019, 15:02
Oui merci.
^2] = E[(y_1-\bar{y} )^2] = \sigma^2 + \sigma^2 - 2E[y_1\bar{y}])
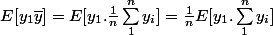
que puis sortir ici ?
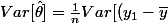^2] = \frac{1}{n} ( Var[(y_1 )^2] +Var[\bar{y}^2]- 2Var[y_i\bar{y]})
)
Je vois pas comment sortir les termes doubles


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Jan 2019, 15:13
par Lostounet » 22 Jan 2019, 15:13
Où a disparu la somme dans l'espérance???
Je te rappelle que les termes
)
ne sont pas tous égaux pour que le 1/n disparaisse...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Jan 2019, 15:18
par Lostounet » 22 Jan 2019, 15:18
^2] = \frac{1}{n} E(\sum_1^n (y_i-\bar{y} )^2)<br />= \frac{1}{n} E(\sum_1^n (y_i^2 - 2y_i \bar{y} + \bar{y}^2)))
= ....
Mais il me semble que c'est pas ça que tu veux calculer.
Tu cherches
^2)
?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 15:32
par fioldodidi » 22 Jan 2019, 15:32
Merci !
^2] = \frac{1}{n} E(\sum_1^n (y_i-\bar{y} )^2)<br />= E[y_1^2]- 2E[y_1\bar{y} ]+ E[(\frac{1}{n} \sum_1^n y_i)^2]=\sigma^2 - 2E[y_1\bar{y} ]+ \frac{1}{n^2}E[(\sum_1^n y_i)^2)])
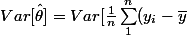^2] = \frac{1}{n^2}(Var[y_1^2]- 2Var[y_1\bar{y} ]+ \frac{1}{n^4}Var[(\sum_1^n y_i)^2]))
J'en suis bloqué ici maintenant.
Modifié en dernier par
fioldodidi le 22 Jan 2019, 15:40, modifié 3 fois.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 15:35
par fioldodidi » 22 Jan 2019, 15:35
Oui que je décompose en biais variance et pour le biais j'ai besoin de E[tetha chapeau]
-
cassiopella
- Membre Naturel
- Messages: 50
- Enregistré le: 20 Jan 2019, 14:47
-
 par cassiopella » 22 Jan 2019, 15:51
par cassiopella » 22 Jan 2019, 15:51
Ton calcul du biais est toujours faux!
Tu oublies les sigmas (somme), c'est pour cela que tu n'arrives pas à simplifier. Je conseille de dévélopper la somme sans sigma pour voir mieux. J'ajoute un étape à la suggestion de @Lostoutnet :
 = \mathbb{E} (\sum_{i=1}^{n} \frac{(y_i - \bar{y})^2}{n}) = \mathbb{E} (\frac{1}{n} \cdot \sum_{i=1}^{n} (y_i - \bar{y})^2) =\frac{1}{n} \cdot \mathbb{E}\Big[ (y_1 - \bar{y})^2 + (y_2 - \bar{y})^2 + ... + (y_{n-1} - \bar{y})^2 + (y_n - \bar{y})^2 \Big])
 = \frac{1}{n} \cdot \mathbb{E}\Big[ y_{1}^{2} + 2y_1 \bar{y} + \bar{y}^{2} + y_{2}^{2} + 2y_2 \bar{y} + \bar{y}^{2} + ... + y_{n-1}^{2} + 2y_{n-1} \bar{y} + \bar{y} ^{2}+ y_{n}^{2} + 2y_n \bar{y} + \bar{y}^{2} \Big] = ...)
 = \frac{1}{n} \cdot \mathbb{E}\Big[ (y_{1}^{2} + y_{2}^{2} +...+y_{n-1}^{2} +y_{n}^{2}) +( 2y_1 \bar{y} + 2y_2 \bar{y} + ... + 2y_{n-1} \bar{y} + 2y_n \bar{y}) + ( \bar{y}^{2} + \bar{y}^{2} +...+ \bar{y}^{2} + \bar{y}^{2} ) \Big] = ...)
Il ne faut pas hésiter de dévélopper quand tu n'as pas encore les automatismes.
Modifié en dernier par
cassiopella le 22 Jan 2019, 15:58, modifié 1 fois.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 15:57
par fioldodidi » 22 Jan 2019, 15:57
Pour moi :
 = \frac{1}{n} \cdot \mathbb{E}\Big[ y_{1}^{2} + 2y_1 \bar{y} + \bar{y} + y_{2}^{2} + 2y_2 \bar{y} + \bar{y}^2 + ... + y_{n-1}^{2} + 2y_{n-1} \bar{y} + \bar{y}^2 + y_{n}^{2} + 2y_n \bar{y} + \bar{y}^2 \Big] = \frac{1}{n} (n*E[y_1^2]- 2*n*E[y_1\bar{y} ]+ n*E[\bar{y}^2]) = E[y_1^2]- 2E[y_1\bar{y} ]+ E[(\frac{1}{n} \sum_1^n y_i)^2])
Modifié en dernier par
fioldodidi le 22 Jan 2019, 15:59, modifié 1 fois.
-
cassiopella
- Membre Naturel
- Messages: 50
- Enregistré le: 20 Jan 2019, 14:47
-
 par cassiopella » 22 Jan 2019, 15:58
par cassiopella » 22 Jan 2019, 15:58
Oui, j'ai corrigé.
Modifié en dernier par
cassiopella le 22 Jan 2019, 16:00, modifié 2 fois.
-
fioldodidi
- Membre Naturel
- Messages: 21
- Enregistré le: 13 Oct 2017, 15:44
-
 par fioldodidi » 22 Jan 2019, 15:59
par fioldodidi » 22 Jan 2019, 15:59
Donc c'est quoi mon problème, j'ai la même chose non ?
^2] = \frac{1}{n} E(\sum_1^n (y_i-\bar{y} )^2)<br />= E[y_1^2]- 2E[y_1\bar{y} ]+ E[(\frac{1}{n} \sum_1^n y_i)^2]=\sigma^2 - 2E[y_1\bar{y} ]+ \frac{1}{n^2}E[(\sum_1^n y_i)^2)])
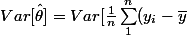^2] = \frac{1}{n^2}(Var[y_1^2]- 2Var[y_1\bar{y} ]+ \frac{1}{n^4}Var[(\sum_1^n y_i)^2]))
J'en suis bloqué ici maintenant.
-
cassiopella
- Membre Naturel
- Messages: 50
- Enregistré le: 20 Jan 2019, 14:47
-
 par cassiopella » 22 Jan 2019, 16:01
par cassiopella » 22 Jan 2019, 16:01
Il ne faut pas développer la moyenne, au contraire. Le terme du milieu, la somme des
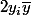
, tu ne vois pas ce que c'est? Par quoi tu peux factoriser ici :
)
Et déjà l’espérance de la somme c'est ... ?
-
cassiopella
- Membre Naturel
- Messages: 50
- Enregistré le: 20 Jan 2019, 14:47
-
 par cassiopella » 22 Jan 2019, 16:10
par cassiopella » 22 Jan 2019, 16:10
Bon, pour la variance je donne l'expréssion finale que tu dois obtenir si tu simplifies la somme :
^2}{n} = ... = \Big[ \sum_{i=1}^{n} \frac{y_{i}^{2}}{n} \Big]- \bar{y}^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
