Erreur d'approximation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 17 Fév 2020, 20:32
Bonjour à tous,
=\frac{1}{1+x^2})
.
=-\frac 4 5 x^2+1)
et
=-\frac 2 3 x^2+1)
sont les polynômes interpolateurs de Lagrange de f respectivement en -0.5, 0, 0.5 et en
, 0,
.
L'intégrale entre -1 et 1 de p_2 est plus proche de l'intégrale entre -1 et 1 de f que l'intégrale entre -1 et 1 de p_1.
Je remarque que les trois fonctions sont positives sur [-1; 1].
Peut-on en déduire que p_2 est une meilleure approximation de f que p_1 l'est ? En vertu de quel théorème ?
Merci bcp de votre aide !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6141
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 18 Fév 2020, 10:29
La question est : quelle norme te donnes-tu sur l'espace des fonctions (continues, ou
, ou ...) sur
?
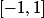
Cette norme quantifiera la distance, et tu pourras alors dire qui est le plus proche.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
