Ou est l'erreur ??
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 09:53
par nada-top » 29 Aoû 2006, 09:53
[FONT=Palatino Linotype]Bonjour,[/FONT]je cherche à démontrer par réccurence que
)=2^n)
avec
 = n)
.
cette question a été posée dans un de mes DS mais j'ai pas eu le corrigé et il y avait une erreur dans mon raisonnement , je me rappelle pas de la preuve de mon prof mais il m'a dit que je vais voir ça en prepa ...
alors voilà mon raisonnement :
pour

on a
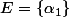
donc
=\{\{\alpha_1\} , \empty \})
donc la propriété est vérifiée.
-suposons que
)=2^n)
et démontrons que
)=2^{n+1})
tel que
=n+1)
.
donc on a
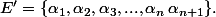
donc

or
) = 2^n)
et
 )= 2)
donc
)=2^n.2=2^{n+1}.)
enfin par réccurence on peut on déduire que
) = 2^n.)
ou est donc l'erreur ?!! :doh:
[FONT=Palatino Linotype]Merci[/FONT]:lol3:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 09:54
par nox » 29 Aoû 2006, 09:54
nada-top a écrit:je cherche à démontrer par réccurence que le nombre des élément de
)
tel que

est

.
erf...manque pas qq chose la ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:00
par nada-top » 29 Aoû 2006, 10:00
comme quoi par exemple ? avec E est fini bien sur , sinon je vois pas :doh:
on a
) = 2^{card(E)})
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 10:05
par nox » 29 Aoû 2006, 10:05
non en fait c'était juste une erreur de formulation :happy2:
"avec E={a1,...an}" plutot que "tel que E{a1,...,an}" non?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:07
par nada-top » 29 Aoû 2006, 10:07
ah oui :ptdr: c'est réglé
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 10:08
par nox » 29 Aoû 2006, 10:08
et euh pourquoi tu dis qu'il y a une erreur? :hein:
(j'ai l'impression que je pose plus de questions que je donne de réponses moi :ptdr:)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 29 Aoû 2006, 10:14
par Flodelarab » 29 Aoû 2006, 10:14
nada-top a écrit: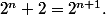
ou est donc l'erreur ?!! :doh:
ahahaha! quel humour !
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:16
par nada-top » 29 Aoû 2006, 10:16
il y a une erreur dans mon raisonnement (d'aprés mon prof) mais je sais pas laquelle tout ce que je sais que j'ai pas eu toute la note sur cette question :cry:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:19
par nada-top » 29 Aoû 2006, 10:19
Flodelarabe a écrit:ahahaha! quel humour !
peux-tu t'expliquer , car effectivement je m'en doute de la conclusion .
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:28
par nada-top » 29 Aoû 2006, 10:28
Arf quelle belle erreur :euh: c'est
) = 2^n . 2 =2^{n+1})
,
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 10:28
par nox » 29 Aoû 2006, 10:28
:ptdr:
tain jvais me flageller pour pas avoir vu ca
:ptdr:
ca marche tout de suite bcp mieux ^^
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:35
par nada-top » 29 Aoû 2006, 10:35
mais si je me rappelle c'était surement pas ça l"erreur :triste: ...l'erreur c'est dans la manière de conclure card(P(E')) , désolée je me rappelle pas trés bien de mon raisonnement .
sinon comment peut on conclure le cardinal P(E') sachant le cardinal de P(E )et
)
et que
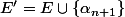
??
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 10:50
par nox » 29 Aoû 2006, 10:50
sinon euh...le
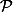
ca représente quoi exactement? :briques:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 10:51
par nada-top » 29 Aoû 2006, 10:51
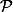
c'est l'ensemble des partie
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 29 Aoû 2006, 10:54
par nox » 29 Aoû 2006, 10:54
ok ba alors ca marche...
ca me parait logique en tout cas. A chaque partie de E tu peux ajouter a1 donc le nombre de parties de E est multiplié par 2.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 11:08
par nada-top » 29 Aoû 2006, 11:08
oui c'est à peu prés à ça que j'ai pensé mais je vois pas encore ou réside le probleme?? :hein:
vraiment je me rappelle pas trés bien comment j'ai conclu

mais il me parait que je me suis servi d'un truc de dénombrement .
je crois que si on répond à ça tout s'explique :
comment peut on conclure le cardinal de P(E') sachant le cardinal de
P(E )et
)
et que
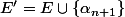
??
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 29 Aoû 2006, 11:23
par kazeriahm » 29 Aoû 2006, 11:23
bah le truc c'est que tu dis que card(P(A U B))= card(P(A))*card(P(B)), ce qui est faux
par exemple E de cardinal n, F contenu dans E non vide de cardinal mon a E U F =E donc card(P(E U F))=2^n différent de 2^(n+m).
enfin en l'occurence tes deux ensembles sont disjoints mais je suis pas sur que t'ais le droit non plus
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 11:28
par nada-top » 29 Aoû 2006, 11:28
non non vraiment désolée mais je crois que j'ai conclue
) = 2^n +2^n = 2^{n+1})
..j'essaye de me rappeller comment :ptdr:
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 29 Aoû 2006, 11:30
par raptor77 » 29 Aoû 2006, 11:30
Tu as oublié un accent grave au u de ou (ca devrait être où)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 29 Aoû 2006, 11:31
par Flodelarab » 29 Aoû 2006, 11:31
Je ne vois pas pkoi tu veux faire ça par récurrence.
pour faire une partie de E de card n, il faut choisir i élément parmi n indépendemment de l'ordre et sans répétition. en additionnant les quantités de parties possible, on a la réponse:
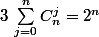
...
Si tu tiens vraiment a la récurrence, tu peux dire qu'a chaque rang tu ajoutes aux parties déjà trouvées (

parties) les parties qui comprennent maintenant le nouvel élément (

parties)
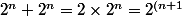})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
