équivalent

[celahesss]

je cherche un équivalent d (k parmi n) = n!/(k!*(n-k)!) lorsque n tend vers + infinie
si vous pouvez m'aider ?
merci d'avance

[COTLOD]

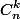
Pour un équivalent de je pense qu'il faut développer et garder le terme de plus haut degré en n.

[leon1789]

je cherche un équivalent d (k parmi n) = n!/(k!*(n-k)!) lorsque n tend vers + infinie

pour k fixé ? (j'espère)
Dans ce cas, est un polynôme en n, dont on peut facilement connaître le monôme dominant.

[Black Jack]

n!/(k!*(n-k)!)

n!/(n-k)! = n*(n-1)*(n-2)*...*(n-k+1)
n!/(n-k)! = n^k +/- des puissances de n inférieures à k

lim(n -> +oo) [n!/(n-k)!) ] = lim(n -> +oo) [n^k]

Et donc ...

:zen: