équations différentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 16 Juin 2008, 18:11
par legeniedesalpages » 16 Juin 2008, 18:11
Bonsoir,
je commence à voir les équations différentielles et j'ai un peu de mal.
Pour les équations du type

avec
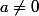
c'est ok.
Je commence ensuite à rencontrer des problèmes avec ce genre d'équations:
:\ af'+bf=0)
(toujours avec
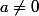
)
ie

ie
 =-\frac{b}{a} f(t),\ \forall t\in \mathbb{R})
si

ne s'annule pas j'aurai tendance à continuer en faisant

,
mais si

s'annule on peut faire ça, comment on s'en sort, il doit pourtant bien y avoir des équa diff de ce type qui ont des solutions admettant des zéros :hein:
Merci pour votre aide.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Juin 2008, 18:15
par ThSQ » 16 Juin 2008, 18:15
legeniedesalpages a écrit:mais si

s'annule on peut faire ça, comment on s'en sort, il doit pourtant bien y avoir des équa diff de ce type qui ont des solutions admettant des zéros :hein:
Merci pour votre aide.
Oui, d'ailleurs f=0 ne convient-il pas ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Juin 2008, 18:16
par fatal_error » 16 Juin 2008, 18:16
Salut,
Si f s'annule pour une valeur alors on a
=0 => f'(t_0)=0)
donc ca vérifie leq donc c'est pas grave.
Enfin, je pense.
la vie est une fête

 par legeniedesalpages » 16 Juin 2008, 18:19
par legeniedesalpages » 16 Juin 2008, 18:19
Salut ThsQ,
oui c'est vrai, mais alors comment résoud-on ce genre d'équa diff sans négliger ces solutions, peut-on aboutir à quelque chose à partir de cette relation:
 =-\frac{b}{a} f(t),\ \forall t\in \mathbb{R})
 par legeniedesalpages » 16 Juin 2008, 18:23
par legeniedesalpages » 16 Juin 2008, 18:23
fatal_error a écrit:Salut,
Si f s'annule pour une valeur alors on a
=0 => f'(t_0)=0)
donc ca vérifie leq donc c'est pas grave.
Enfin, je pense.
ok donc les relations
 =-\frac{b}{a} f(t),\ \forall t\in \mathbb{R})
et
 =-\frac{b}{a} f(t),\ \forall t\in \mathbb{R}:\ f(t)\neq 0)
seraient équivalentes.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Juin 2008, 18:27
par fatal_error » 16 Juin 2008, 18:27
Ca n'engage que moi, mais je dirais oui.
De plus, on a jamais fait la dissociation pour les cas ou f s'annule en TD ce qui serait une assez grosse boulette donc je pense que les deux relations donnent les même solutions
la vie est une fête

 par legeniedesalpages » 16 Juin 2008, 18:42
par legeniedesalpages » 16 Juin 2008, 18:42
fatal_error a écrit:Ca n'engage que moi, mais je dirais oui.
De plus, on a jamais fait la dissociation pour les cas ou f s'annule en TD ce qui serait une assez grosse boulette donc je pense que les deux relations donnent les même solutions
ok merci j'adopte

(j'ai encore jamais eu de td d'équa diff au bout d'une licence, ils doivent pas aimer ça dans ma fac, ou peut être qu'ils nous en parleront un peu en master ^^ ).
Donc je reprend à partir de la relation

,
ie
' = -\frac{b}{a})
,
ie
'(t) dt = -\frac{b}{a} \Bigint dt,\qquad \forall t\in \mathbb{R}:\ f(t)\neq 0)
,
ie
(t) = -\frac{b}{a} t+C,\qquad \forall t\in \mathbb{R}:\ f(t)\neq 0)
où C est une constante réelle,
ie
|=e^C e^{-\frac{b}{a} t},\qquad \forall t\in \mathbb{R}:\ f(t)\neq 0)
,
et là je ne vois pas comment virer la valeur absolue :hein:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Juin 2008, 19:06
par fatal_error » 16 Juin 2008, 19:06
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Juin 2008, 20:37
par fatal_error » 16 Juin 2008, 20:37
Ah,
"toute solution de H est soit identiquement nulle soit ne s'annulant pas sur I".
Désolé pour legenie, et merci pour le polycopié par la même occasion :-).
la vie est une fête

-
jiji_1987
- Messages: 2
- Enregistré le: 20 Juin 2008, 18:44
-
 par jiji_1987 » 20 Juin 2008, 18:53
par jiji_1987 » 20 Juin 2008, 18:53
bonjour je suis etudiante en premiere annee de la fac et je veux savoir comment resoudre cet exercice svp :
On cherche a résoudre l'équation différentielle :
(Ey): y''+2xy'+(x²_3)y=exp (_x²/2)
soit y une fonction on définit alors la fonction z en posant y= exp (_x²/2)z.
1)Montrer que y est solution de (Ey) si et seulement si
z vérifie z''_4z=1
on considère l'équation différentielle (Ez):z''_4z=1
2)
a) Trouver une fonction constante z=k solution de (Ez)
b)résoudre l'équation différentielle(Ez)
3)déduire de 1) et 2) les solutions de (Ey)
-
mathelot
 par mathelot » 20 Juin 2008, 20:16
par mathelot » 20 Juin 2008, 20:16
bonsoir,
y et z représentent des fonctions dérivables. Sais-tu dériver un produit ?
-
jiji_1987
- Messages: 2
- Enregistré le: 20 Juin 2008, 18:44
-
 par jiji_1987 » 20 Juin 2008, 22:50
par jiji_1987 » 20 Juin 2008, 22:50
[quote="mathelot"]bonsoir,
y et z représentent des fonctions dérivables. Sais-tu dériver un produit ?[/QUOTE *
oui je sais derive un produit mais je vois pas ce que tu veux dire si tu m'expliquer plus car avec notre prof de td on jamais fat ce genre d'exo et j'en ai jamais trouve svp
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités