Bonjour,
je sollicite votre aide pour résoudre ces 4 exercices car j'ai vraiment du mal à les résoudre.
(En gras lénoncé et en normal ce que j'ai fais.)
Resoudre les equations differentielles suivantes sur R:
Question 1
{ y'-2y=e^x
{ y(0)=1
donc j'ai appliqué la formule tq: y'-ay=b
f(x)=K e^(ax) - b/a
f(x)=K e^(2x) - (e^x)/-2
=K e^(2x) + (e^x)/2
f(0)=K e^(2*0) + (e^0)/2=1
=K=1
donc f(x)=1e^(2x) + (e^x)/2
Question 2
{ (1+x^2)y' - 2xy = x
{ y(0)=0
j'ai diviser la 1ere ligne par (1+x^2), pour avoir une equation du type y'-ay=b ce qui donne:
y'- (2 * ( 1/(1+x^2) )xy=x/(1+x^2)
f(x)=Ke^(2 * ( 1/(1+x^2) ) - [(x/1+x^2) / (2 * ( 1/(1+x^2) )]
f(0)=K e^2=0
K=e^(-2)
donc f(x)=(e^(-2)) e^(2 * ( 1/(1+x^2) ) - [(x/1+x^2) / (2 * ( 1/(1+x^2) )]
Question 3
{ y"-4y'+3y=0
Je ne n'arrive pas à le résoudre car le y" me bloque et je ne sais pas comment procéder
Question 4
{ y"-4y'+3y=0 (On pourra chercher une solution particulière de cette équation de la forme (ax+b)e^(2x) )
Pareil, je ne n'arrive pas à le résoudre car le y" me bloque et je ne sais pas comment procéder
si vous pouvez me donnez un coup de pouce, je vous en serrai reconnaissant.
cordialement
Equations differentielles
5 messages
- Page 1 sur 1
À coefficients constants
Elles sont de la forme où a, b et c sont des réels, a non nul.
où a, b et c sont des réels, a non nul.
On cherche des solutions sous forme exponentielle, cest-à-dire telles que = e^{\lambda x}) . Une telle fonction sera solution de léquation différentielle si et seulement si delta est solution de
. Une telle fonction sera solution de léquation différentielle si et seulement si delta est solution de
:
Cette équation est appelée équation caractéristique de léquation différentielle.
Comme pour toute équation du second degré, trois cas se présentent selon le signe du discriminant delta.
Si \delta > 0
Léquation possède deux solutions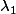 et
et 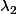 .
.
Léquation possède au moins deux fonctions exponentielles solutions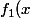 = e^{\lambda_1x}) et
et  = e^{\lambda_2x}) . On démontre que ces deux solutions famille génératrice|engendrent lensemble des solutions. Cest-à-dire que lensemble des solutions sont les fonctions définies sur R par
. On démontre que ces deux solutions famille génératrice|engendrent lensemble des solutions. Cest-à-dire que lensemble des solutions sont les fonctions définies sur R par  = C_1f_1(x) + C_2f_2(x)) où
où  et
et  sont deux réels quelconques.
sont deux réels quelconques.
Pour déterminer ces deux constantes, il est naturel de donner deux informations sur la fonction
* cela se fait en général en donnant des conditions initiales en un point , cest-à-dire en précisant les valeurs
, cest-à-dire en précisant les valeurs  et
et  de y et y à cet instant. Dans ce cas lexistence et lunicité de la solution vérifiant ces conditions initiales sont garanties.
de y et y à cet instant. Dans ce cas lexistence et lunicité de la solution vérifiant ces conditions initiales sont garanties.
* pour de nombreux problèmes physiques, il est fréquent de donner des conditions aux limites en précisant les valeurs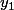 et
et 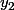 aux instants
aux instants  et
et  . Il y a alors fréquemment existence et unicité des solutions, mais ce nest pas toujours vrai.
. Il y a alors fréquemment existence et unicité des solutions, mais ce nest pas toujours vrai.
Si delta = 0
Léquation ne possède quune seule solution delta. On démontre alors que lensemble des solutions sont les fonctions f définies sur R par = (Ax + B)e^{\lambda x}) où A et B sont des réels quelconques.
où A et B sont des réels quelconques.
Pour déterminer A et B, il faut, comme dans le cas précédent posséder deux informations sur f.
Si delta < 0
Léquation ne possède pas de solutions réelles mais deux solutions complexes :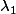 et
et 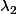 conjuguées lune de lautre.
conjuguées lune de lautre.
Il est alors utile de faire une incursion dans les fonctions définies sur R et à valeurs dans C. Les fonctions et
et  définies par
définies par 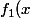 = e^{\lambda_1x}) et
et  = e^{\lambda_2x}) sont des solutions de léquation dans cet ensemble. On démontre alors que lensemble des fonctions de R dans C solutions de léquation différentielle sont les fonctions définies par
sont des solutions de léquation dans cet ensemble. On démontre alors que lensemble des fonctions de R dans C solutions de léquation différentielle sont les fonctions définies par  = C_1e^{\lambda_1x} + C_2e^{\lambda_2x}) où
où  et
et  sont deux complexes quelconques.
sont deux complexes quelconques.
Cependant, on cherche encore des fonctions à valeurs dans R. On note alors . Les fonctions
. Les fonctions  et
et  sécrivent alors
sécrivent alors
: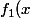 = e^{ux} (\cos(vx) + i\sin(vx))\,)
: = e^{ux} (\cos(vx) - i\sin(vx))\,) .
.
On peut alors remarquer que les fonctions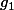 et
et 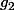 définies par
définies par
: =\frac 12 (f_1(x) + f_2(x) )= e^{ux}\cos(vx))
: = \frac{1}{2i}(f_1(x) - f_2(x)) = e^{ux}\sin(vx))
sont encore des solutions de léquation différentielles mais à valeurs dans R. On démontre alors quelles engendrent lensemble des solutions à valeurs dans R cest-à-dire que cet ensemble est formé des fonctions définies sur R par
: = e^{ux}(A\cos(vx) + B\sin(vx))\,) où A et B sont deux réels quelconques.
où A et B sont deux réels quelconques.
Remarque : on peut écrire cette solution sous la forme : = q e^{ux}\cos(vx+r)\,) ,q et r sont deux réels quelconques (cette forme est parfois plus pratique).
,q et r sont deux réels quelconques (cette forme est parfois plus pratique).
La détermination de A et B (ou q et r) se fait, comme dans les cas précédents, par la donnée de deux informations sur f.
Elles sont de la forme
On cherche des solutions sous forme exponentielle, cest-à-dire telles que
:
Cette équation est appelée équation caractéristique de léquation différentielle.
Comme pour toute équation du second degré, trois cas se présentent selon le signe du discriminant delta.
Si \delta > 0
Léquation possède deux solutions
Léquation possède au moins deux fonctions exponentielles solutions
Pour déterminer ces deux constantes, il est naturel de donner deux informations sur la fonction
* cela se fait en général en donnant des conditions initiales en un point
* pour de nombreux problèmes physiques, il est fréquent de donner des conditions aux limites en précisant les valeurs
Si delta = 0
Léquation ne possède quune seule solution delta. On démontre alors que lensemble des solutions sont les fonctions f définies sur R par
Pour déterminer A et B, il faut, comme dans le cas précédent posséder deux informations sur f.
Si delta < 0
Léquation ne possède pas de solutions réelles mais deux solutions complexes :
Il est alors utile de faire une incursion dans les fonctions définies sur R et à valeurs dans C. Les fonctions
Cependant, on cherche encore des fonctions à valeurs dans R. On note alors
:
:
On peut alors remarquer que les fonctions
:
:
sont encore des solutions de léquation différentielles mais à valeurs dans R. On démontre alors quelles engendrent lensemble des solutions à valeurs dans R cest-à-dire que cet ensemble est formé des fonctions définies sur R par
:
Remarque : on peut écrire cette solution sous la forme :
La détermination de A et B (ou q et r) se fait, comme dans les cas précédents, par la donnée de deux informations sur f.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 161 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
