Equation d'une courbe à partir de points
16 messages
- Page 1 sur 1
equation d'une courbe à partir de points
je voudrais trouver l'equation de la courbe qui passe par les points suivants :
y x
0,823388267 310,1570681
0,736164933 309,3193717
0,593750558 304,8167539
0,528555892 292,9842932
0,5053669 278,0104712
0,4635761 219,895288
0,4 0
A l'aide d'une fonction polynomiale d'ordre 6 j'obtient une courbe qui passe par les 7 points. Par contre, si je prends une valeur de x qui n'est pas dans ce tableau j'obtient une valeur de y complétement fausse.
J'ai essayé avec les courbes de tendance d'excel mais cela ne donne rien de précis.
Existe-t-il un logiciel ou une méthode pour trouver cette équation ?
Je précise que les points proviennent de mesures.
Merci d'avance pour votre aide
y x
0,823388267 310,1570681
0,736164933 309,3193717
0,593750558 304,8167539
0,528555892 292,9842932
0,5053669 278,0104712
0,4635761 219,895288
0,4 0
A l'aide d'une fonction polynomiale d'ordre 6 j'obtient une courbe qui passe par les 7 points. Par contre, si je prends une valeur de x qui n'est pas dans ce tableau j'obtient une valeur de y complétement fausse.
J'ai essayé avec les courbes de tendance d'excel mais cela ne donne rien de précis.
Existe-t-il un logiciel ou une méthode pour trouver cette équation ?
Je précise que les points proviennent de mesures.
Merci d'avance pour votre aide
le tableau correspond à des mesures que j'ai effectué sur un systéme.
A partir de ces points, j'ai tracé la courbe avec excel (nuage de points+lissage). L'allure que j'obtiens correspond à celle théorique donné dans des bouquins.
Maintenant j'ai besoin de l'équation de cette courbe pour l'utiliser toujours sur excel dans d'autres calculs.
A partir de ces points, j'ai tracé la courbe avec excel (nuage de points+lissage). L'allure que j'obtiens correspond à celle théorique donné dans des bouquins.
Maintenant j'ai besoin de l'équation de cette courbe pour l'utiliser toujours sur excel dans d'autres calculs.
Donc tu cherches l'approximation d'une courbe plus qu'une simple interpooation.
Je ne m'y connais pas trop mais tu peux essayer des interpolations avec plus de poitns (tirés de ta courbe excel). En faisant des essais en augmentant le degré du polynôme interpolateur tu pourras peut être parvenir à quelque chose.
Je ne m'y connais pas trop mais tu peux essayer des interpolations avec plus de poitns (tirés de ta courbe excel). En faisant des essais en augmentant le degré du polynôme interpolateur tu pourras peut être parvenir à quelque chose.
j'ai rajouté des points dans la 1ére partie et j'arrive à une fct d'ordre 10.
Mais j'ai toujours le même probleme, par exemple pour x = 200 (valeur hors tableau de mesures), j'obtiens - 11 avec la fct d'ordre 10 ?? alors que ma valeur max est de 0,82.
il faudrait sans doute une autre forme d'equation mais laquelle ? Quelqu'un à une idée ?
Mais j'ai toujours le même probleme, par exemple pour x = 200 (valeur hors tableau de mesures), j'obtiens - 11 avec la fct d'ordre 10 ?? alors que ma valeur max est de 0,82.
il faudrait sans doute une autre forme d'equation mais laquelle ? Quelqu'un à une idée ?
Salut,
ton probleme c'est les effet de bord (phénomène de Runge), l'interpolation de lagrange n'est pas stable aux bords des intervalles que tu considère. Pour te rapprocher au maximum, de ta fonction réelle, essaye des mesures avec des points de tchebytchev (ou chebyschev, au choix de toute facon c'est une approximation :we:
pour info les points de subdivision de chebyschev sur [0,1] sont :
\pi}{2n})
Mais attention tu ne sera plus prés qu'à l'interieur de l'intervalle [min xi, max xi]. L'interpolation de lagrange, c'est pour de l'interpolation et ca supporte tres mal l'extrapolation.
Tu peut pour cela t'interresser à l'approximation, plutot qu' l'interpolation. Ainsi tu peut chercher une fonction simple (polynomes par exemple) qui se rapproche le mieux des points de mesures (au sens des moindres carrés)
Pour ton cas, on va chercher à approcher ta fonction par un polynome de degree 5 (au dela on retombe sur une interpolation :happy2: )
 \approx \Bigsum_{i=1}^5{\alpha_i x^{i-1}})
comme ta mesure en x=0, n'a pas l'aire sérieuse (trop loin des autres) il faut pondérer l'erreur à minimiser :
 = \Bigsum_{k=1}^7{\omega_k \left(y_k-\Bigsum_{i=1}^5{\alpha _i x_k^{i-1}}\right)^2})
attention il y les indice i=1..5 des fonction approximante,
et k=1..7 de l'echantillon de mesure.
en notant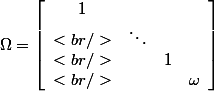 la matrice des poids, et
la matrice des poids, et _{k=1\ldots7,i=1\ldots5}) la matrice 7x5 de la base d'echantillon alors on a les alpha en résolvant le système suivant :
la matrice 7x5 de la base d'echantillon alors on a les alpha en résolvant le système suivant :
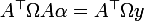
Tu peut fixer w suivant la fiabilité de la dernière mesure, ou le laisser en parametre, ainsi tu aura une famille d'approximation parmis lesquels tu peut choisir celle que tu prefère.
Une base de polynome n'est pas forcément le meilleur choix tu peut essayer avec d'autre fonction. Pour le poids, le mieux c'est de prendre l'inverse de la variance si tu as des erreurs de mesure.
Le mieux pour ce genre de calcul c'est scilab (ou maple pour les calculs formelle)
sinon avec une feuille excel ca se fait aussi (c'est plus long mais ce se fait), tu peut utiliser le module d'optimisation pour minimiser le critère (ca s'appelle solver en anglais, et c'est un add-ins) il n'est pas selectionné par défaut
ton probleme c'est les effet de bord (phénomène de Runge), l'interpolation de lagrange n'est pas stable aux bords des intervalles que tu considère. Pour te rapprocher au maximum, de ta fonction réelle, essaye des mesures avec des points de tchebytchev (ou chebyschev, au choix de toute facon c'est une approximation :we:
pour info les points de subdivision de chebyschev sur [0,1] sont :
Mais attention tu ne sera plus prés qu'à l'interieur de l'intervalle [min xi, max xi]. L'interpolation de lagrange, c'est pour de l'interpolation et ca supporte tres mal l'extrapolation.
Tu peut pour cela t'interresser à l'approximation, plutot qu' l'interpolation. Ainsi tu peut chercher une fonction simple (polynomes par exemple) qui se rapproche le mieux des points de mesures (au sens des moindres carrés)
Pour ton cas, on va chercher à approcher ta fonction par un polynome de degree 5 (au dela on retombe sur une interpolation :happy2: )
comme ta mesure en x=0, n'a pas l'aire sérieuse (trop loin des autres) il faut pondérer l'erreur à minimiser :
attention il y les indice i=1..5 des fonction approximante,
et k=1..7 de l'echantillon de mesure.
en notant
Tu peut fixer w suivant la fiabilité de la dernière mesure, ou le laisser en parametre, ainsi tu aura une famille d'approximation parmis lesquels tu peut choisir celle que tu prefère.
Une base de polynome n'est pas forcément le meilleur choix tu peut essayer avec d'autre fonction. Pour le poids, le mieux c'est de prendre l'inverse de la variance si tu as des erreurs de mesure.
Le mieux pour ce genre de calcul c'est scilab (ou maple pour les calculs formelle)
sinon avec une feuille excel ca se fait aussi (c'est plus long mais ce se fait), tu peut utiliser le module d'optimisation pour minimiser le critère (ca s'appelle solver en anglais, et c'est un add-ins) il n'est pas selectionné par défaut
Scilab est vraiment pratique on peut quasiment tout faire. Il est un peu dure à prendre en main au début, mais si tu connais matlab tu sera pas depaysé.
sinon pour ton approximation les fonctions utils seront:
linsolve(A,b)
vandermonde(v)
pour t'aider à aller plus vite voilà ce que tu peut faire :
et voila le tour est jouer, bon apres y'a plusieurs methodes de résolution (le gradient conjugué,...), tu peut egalement calculer le jacobien pour aider les calculs, surtout dans le cas de modèle non linéaire.
Le dernier cas (leastsqr) te permettra d'utiliser d'autre modèle non forcément linéaire. (il suffit de remplacer l'ecart par 'g(u,t)-y'
essaye avec : = \frac{\lambda_1}{(\lambda_2-t)^{\lambda_4}} + \lambda_3)
Je pense que tu sera pas decu.
si t'a des problème n'hesite pas à consulter l'aide de scilab (celle en ligne). Elle est en anglais mais bourré d'exemple complets. Et pose des question si tu n'y arrive toujours pas
pour les polynomes j'obtiens ca c'est pas joli :

sinon pour ton approximation les fonctions utils seront:
linsolve(A,b)
vandermonde(v)
pour t'aider à aller plus vite voilà ce que tu peut faire :
- Code: Tout sélectionner
//on rentre les données de l'echantillon
//attention on veut des vecteurs colonnes
t=[...]'
y=[...]'
m=size(t,1) // on recupere la taille de l'echantillon
n=... // le nombre de parametre qu'on fais varier (d°polynome-1)
V=vandermonde(t)
A=V(:,1:n) // on ne prend que les n colonnes qui nous interresse
//pour de l'interpolation au choix
// la fonction qui fait tout (ouai)
beta_1 = linsolve(V,y)
//ou le calcul explicite (beurk)
beta_2 = inv(V)*y
// inv(V) plutot que V^-1 car c'est plus rapide
// il diagonalise la matrice et pour une simple inversion ca sert à rien
//pour l'approximation des moindres carrés
//le calcul explicite (beurk)
alpha_2 = inv(A'*A)*A'*y
//la fonction de scilab (ouai)
//simplement
alpha_0 = linsolve(A'*A, A'*y)
//ou plus subtile
//on définie d'abord la fonction de R^n->R^m qu'on cherche a minimiser
function e = f(u)
e=A*u-y //le vecteur des ecarts entre le modele et les mesures
end
uo = zeros(1::n) //une valeur initiale
alpha_1 = leastsqr(f, uo)
et voila le tour est jouer, bon apres y'a plusieurs methodes de résolution (le gradient conjugué,...), tu peut egalement calculer le jacobien pour aider les calculs, surtout dans le cas de modèle non linéaire.
Le dernier cas (leastsqr) te permettra d'utiliser d'autre modèle non forcément linéaire. (il suffit de remplacer l'ecart par 'g(u,t)-y'
essaye avec :
Je pense que tu sera pas decu.
si t'a des problème n'hesite pas à consulter l'aide de scilab (celle en ligne). Elle est en anglais mais bourré d'exemple complets. Et pose des question si tu n'y arrive toujours pas
pour les polynomes j'obtiens ca c'est pas joli :

je me suis trompé vandermonde n'existe pas, mais c'est pas grave, on l'obtient en faisant:
sinon le modèle non linéaire que je t'ai montré à la fin s'ajuste trés bien. J'obtient comme fonction approchante :
 = \frac{0.0002044}{(0.7905573-t)^{1.7661427}}+0.4820013)
ah j'oubliais, j'ai ramener l'echelle sur les t en divisant par 400, ainsi on voit mieux les variations relatives.
et on a le graphique :

- Code: Tout sélectionner
function [v] = vandermonde(x)
n = size(x,1)
v = (x*ones(1,n)).^(ones(n,1)*(0:n-1))
endfunction
sinon le modèle non linéaire que je t'ai montré à la fin s'ajuste trés bien. J'obtient comme fonction approchante :
ah j'oubliais, j'ai ramener l'echelle sur les t en divisant par 400, ainsi on voit mieux les variations relatives.
et on a le graphique :

Création d'une nouvelle équation à partir de deux courbes
Bonjour,
j'ai besoin d'un petit coup de main sur un problème physique.
je dispose deux équation différentes, chacune valable entre deux bornes (équation 1 valable entre borne a et b, équation 2 valable entre borne b et c).
Est-il possible de créer une nouvelle équation valable entre les bornes a et c?
Ma première équation est type affine (y=ax+b), la seconde est plus complexe, de type
1/(a+(b-c)*(d/(x+d)))
Ces deux courbe se coupent en un point commun (borne b)
Merci par avance de vos réponses.
j'ai besoin d'un petit coup de main sur un problème physique.
je dispose deux équation différentes, chacune valable entre deux bornes (équation 1 valable entre borne a et b, équation 2 valable entre borne b et c).
Est-il possible de créer une nouvelle équation valable entre les bornes a et c?
Ma première équation est type affine (y=ax+b), la seconde est plus complexe, de type
1/(a+(b-c)*(d/(x+d)))
Ces deux courbe se coupent en un point commun (borne b)
Merci par avance de vos réponses.
Bonjour,
Ce très vieux sujet est ressorti.
Pour le fun, j'ai essayé de trouver une fonction (méthode automatique).
Ajustement exponentiel Y= A + B * e puis(C * X) A = 317. B = -427321. C = -18.0
En fait, il s'agit de X=f(Y), c'est à dire dans l'ordre habituel de données.
La méthode employée est celle de Jean Jacquelin.
Les résultats sont excellents.
Par contre dans le sens indiqué (X=310 ==> Y=0.82) c'est moins bons. Si le problème était toujours d'actualité, ça justifierait d'affiner la méthode et/ou le calcul.
Ce très vieux sujet est ressorti.
Pour le fun, j'ai essayé de trouver une fonction (méthode automatique).
Ajustement exponentiel Y= A + B * e puis(C * X) A = 317. B = -427321. C = -18.0
En fait, il s'agit de X=f(Y), c'est à dire dans l'ordre habituel de données.
La méthode employée est celle de Jean Jacquelin.
Les résultats sont excellents.
Par contre dans le sens indiqué (X=310 ==> Y=0.82) c'est moins bons. Si le problème était toujours d'actualité, ça justifierait d'affiner la méthode et/ou le calcul.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
