Equation du plan tangent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
par humpf » 29 Mai 2007, 12:14
Re-Bonjour
Le deuxième problème, cette semaine, est l'équation du plan tangent. On nous donne la fonction z= f(x;y) =
, R > 0.
))
est un point arbitraire de la surface t.q
. Il faut montrer que l'équation du plan tangent s'écrit
.
L'équation du plan tangent est de la forme ax + by + c = z.
D'après mes calculs,
)
et
)
Enfin, j'ai
 + y_0^2(z_0^{-1}))
.
Donc, l'équation du plan tangent est:
 -yy_0(z_0^{-1}) + z_0 + x_0^2(z_0^{-1}) + y_0^2(z_0^{-1}))
Et là je suis bloquée :doh: parce que je ne vois pas du tout comment passer au résultat demandé. Est-ce que quelqu'un pourrait m'aider?
Merci :marteau:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 29 Mai 2007, 12:25
et si on multiplie par zo et utilise x0^2 + + = R^2 on n 'a pas le résultat ?
cas particulier de l équation du plan tangent à une quadrique
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
par humpf » 29 Mai 2007, 12:32
Ah ben oui :id: !
J'ai multiplié par
. Et on peut déduire de l'équation de la fonction que
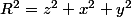
. Et avec tout ça j'arrive au résultat :ptdr:
Mince alors, pour une fois j'étais tout près
Merci beaucoup :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
