Salut,
Une équation différentielle, ça se résout sur un intervalle (*) et pour pouvoir diviser l'équation homogène par
)
, ce dernier doit être non nul, c'est à dire
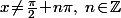
.
Donc on résout en fait sur un (quelconque) des intervalle
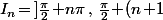\pi[)
.
Et sur cet intervalle là, après calculs, les solutions de l'équation différentielle (avec second membre) sont effectivement les fonctions de la forme
\!=\!\lambda\cos(x)\!+\!x)
où

est une "constante".
Sauf que si on écrit ça tel quel, ben on va droit dans le mur, vu que le fait que

soit une "constante", ce que ça signifie, c'est qu'il ne dépend pas de

, mais par contre il peut évidement dépendre de

: il n'y a pas la moindre raison que la constante soit la même sur chacun des intervalles.
Bref, ce qu'il faut écrire, c'est que les solutions sur l'intervalle

c'est les fonctions de la forme
\!=\!\lambda_n\cos(x)\!+\!x)
où
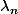
est indépendant de

mais dépend à priori de

.
Ensuite on se pose la question du recollement des solutions et pour donner un exemple concret de la problématique, je te propose ça (et tu fera toi même le cas général) :
On considère la fonction définie sur
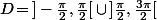
par
=\left\{\begin{matrix}3\cos(x)\!+\!x\text{ si }x\!<\!\frac{\pi}{2}\cr 5\cos(x)\!+\!x\text{ si }x\!>\!\frac{\pi}{2}\end{matrix}\right.)
.
Cette fonction vérifie évidement l'équation différentielle sur D (qui
n'est pas un intervalle), mais,
- Est-elle prolongeable (par continuité) en

?
- Si oui, le prolongement est-il dérivable en

?
- Si oui, le prolongement vérifie-t-il l'équation différentielle en

?
(*) Et ça provient bêtement du fait que le résultat qu'on utilise à longueur de temps, à savoir celui qui dit qu'une fonction dérivable de dérivée partout nulle est forcément constante, ben ce résultat n'est évidement valable QUE sur un intervalle : la fonction définie sur D=R\{0} par f(x)=0 si x<0 et f(x)=1 si x>0 et dérivable sur D, de dérivée partout nulle mais n'est pas constante sur D.
