Equation complexe

[Vuze49]

Bonjour,
quelqu'un peut il me réexpliquer la méthode pour résoudre cet exercice :
"Résoudre dans l'équation sachant qu'une des solutions est réelle et une autre imaginaire pure"
Merci

[busard_des_roseaux]

Bonjour,
quelqu'un peut il me réexpliquer la méthode pour résoudre cet exercice :
"Résoudre dans l'équation sachant qu'une des solutions est réelle et une autre imaginaire pure"
Merci

aloha,

a-priori, en remplaçant z par
et en séparant partie réelle et imaginaire
on trouve deux équations, une de degré 4,
et une de degré 3 en

[busard_des_roseaux]

re,



en remplaçant z par

on trouve deux équations respectivement de degré 4 et de degré 3

et

mais les équations comportent des polynômes et l'on peut effectuer
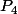
la division euclidienne de par

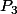
[Decebal]

Bonjour,
quelqu'un peut il me réexpliquer la méthode pour résoudre cet exercice :
"Résoudre dans l'équation sachant qu'une des solutions est réelle et une autre imaginaire pure"
Merci

Bonjour!
Notez qu'il ya une racine z = 5 et les trois autres complexes de la forme a + bi.Nous essayons de trouver une racine complexe pour laquelle a = 0 et de trouver qu'il est z =- 3i.Puis résoudre une équation de degré 2, qui ne présente pas de difficultés à résoudre.
Les racines de l'équation sont