équation autonome

[zaidoun]

Bonsoir,
J'ai un petit exercice:
Soit f: R --> R une application k-lipschitzienne (k>0) et x_0 dans R, on considère le problème de Cauchy
x'(t)= f(x(t)), x(0)= x_0.
1) Montrer que ce problème admet une unique solution maximale x définie sur I
2) Montrer que
|x(t) - x_0 | <= |t| |f(x_0) | e^{k |t |} pour tout t dans I.
3)En déduire que x est définie sur R.


Le 1) est une application du théorème du Cauchy-Lipschitz
Pour 2) je pense qu'on va utiliser Lemme de Grönwall.
Je suis bloqué au 3ème question. Qui peut m'aider?
Merci d'avance.

[mathelot]

est bornée sur tout compact.

R est localement compact.

l'ensemble des tels que
il existe un voisinage de t_0 , tel que on peut prolonger x
sur est ouvert , fermé , non vide. C'est donc R tout entier.

[marawita1]

est bornée sur tout compact.

R est localement compact.

l'ensemble des tels que
il existe un voisinage de t_0 , tel que on peut prolonger x
sur est ouvert , fermé , non vide. C'est donc R tout entier.

Pouvez vous m'expliquer encore, car je n'ai pas bien compris votre réponse.

[mathelot]

Sous les hypothèses "F localement lipschiztienne"
une solution x bornée dans un voisinage de se prolonge au delà de
être localement bornée est un fermé car R est localement compact
et être prolongeable est un ouvert
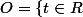/ x est prolongeable au delà de t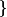
/ Il existe un voisinage V de t tel que x est bornée sur V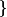

SI alors ou
à confirmer.