Equa diff et transformée de Laplace
15 messages
- Page 1 sur 1
Equa diff et transformée de Laplace
Bonjour à tous,
Je suis bloqué sur la transformée de Laplace d'une équation différentielle, mes souvenirs de cette
méthode remontent à trente ans....Voici l'équation:
y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t) la transformée de Laplace de cette équa diff est:
p².Y(p)+2p.Y(p)+5.Y(p)=2p*(p/(p²+4))*(1/(p-1))
Y(p)*(p²+2p+5)=(2p²)/((p²+4)*(p-1))
Y(p)=(2p²)/((p²+4)*(p-1)*(p²+2p+5))
je pense que ces dernières lignes sont fausses car il est très difficile de décomposer en éléments simples cette fraction. Pouvez-vous m'aider?
Cordialement lefouineur
Je suis bloqué sur la transformée de Laplace d'une équation différentielle, mes souvenirs de cette
méthode remontent à trente ans....Voici l'équation:
y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t) la transformée de Laplace de cette équa diff est:
p².Y(p)+2p.Y(p)+5.Y(p)=2p*(p/(p²+4))*(1/(p-1))
Y(p)*(p²+2p+5)=(2p²)/((p²+4)*(p-1))
Y(p)=(2p²)/((p²+4)*(p-1)*(p²+2p+5))
je pense que ces dernières lignes sont fausses car il est très difficile de décomposer en éléments simples cette fraction. Pouvez-vous m'aider?
Cordialement lefouineur
Re: Equa diff et transformée de Laplace
Bonsoir,
Tu peux peut être demander à 'Wolfram alpha' de décomposer la fraction en éléments simples.
Syntaxe latex \frac{a}{b} pour les fractions et \times pour le signe de multiplication
Tu peux peut être demander à 'Wolfram alpha' de décomposer la fraction en éléments simples.
Syntaxe latex \frac{a}{b} pour les fractions et \times pour le signe de multiplication
Re: Equa diff et transformée de Laplace
Bonjour,
ne manque-t-il pas les conditions initiales[y(0) et y'(0)]?
ne manque-t-il pas les conditions initiales[y(0) et y'(0)]?
Re: Equa diff et transformée de Laplace
Bonjour,
Je pense que la transformée de Laplace donnée par lefouineur n'est pas correcte.
Si c'est bien le cas, il vaudrait mieux la corriger avant de décomposer en éléments simples.
Ceci dit, la résolution de l'équation différentielle est facile sans utiliser Laplace.

Je pense que la transformée de Laplace donnée par lefouineur n'est pas correcte.
Si c'est bien le cas, il vaudrait mieux la corriger avant de décomposer en éléments simples.
Ceci dit, la résolution de l'équation différentielle est facile sans utiliser Laplace.
Re: Equa diff et transformée de Laplace
Rebonjour,
Sans Laplace :
y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t)
Solutions de y"+2y'+5y = 0
r²+2r+5=0
r = -1 +/- 2i
y = e^-t * (A.cos(2t) + B.sin(2t))
----
Solution particulière de y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t)
de la forme : y = e^-t * [(ax + b)*cos(2x) + (cx² + d.x + f).sin(2x)]
y' = ...
y'' = ...
on remet dans l'équation de départ et on identifie les coefficients de même puissance en x des 2 membres
et après de longs calculs embêtants mais sans difficultés réelles, on devrait arriver à :
y = e^(-x) * [(x²/4 - 1/32).sin(2x) + x/8 * cos(2x)]
----
Solutions générales de y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t) :
y = e^-t * (A.cos(2t) + B.sin(2t)) + e^(-x) * [(x²/4 - 1/32).sin(2x) + x/8 * cos(2x)]
Toutes erreurs incluses.

Sans Laplace :
y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t)
Solutions de y"+2y'+5y = 0
r²+2r+5=0
r = -1 +/- 2i
y = e^-t * (A.cos(2t) + B.sin(2t))
----
Solution particulière de y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t)
de la forme : y = e^-t * [(ax + b)*cos(2x) + (cx² + d.x + f).sin(2x)]
y' = ...
y'' = ...
on remet dans l'équation de départ et on identifie les coefficients de même puissance en x des 2 membres
et après de longs calculs embêtants mais sans difficultés réelles, on devrait arriver à :
y = e^(-x) * [(x²/4 - 1/32).sin(2x) + x/8 * cos(2x)]
----
Solutions générales de y"(t)+2y'(t)+5y(t)=2t*(e^-t)*cos(2t) :
y = e^-t * (A.cos(2t) + B.sin(2t)) + e^(-x) * [(x²/4 - 1/32).sin(2x) + x/8 * cos(2x)]
Toutes erreurs incluses.
Re: Equa diff et transformée de Laplace
Bonsoir mathelot, Pisigma et Black Jack, et merci pour vos réponses rapides.
@mathelot: décomposer une fraction rationnelle en éléments simples, ma calculette sait le faire, et moi aussi.
@Pisigma: je pense aussi qu'il manque à mon équation en p les conditions initiales mais l'énoncé ne les donne pas.
@Black Jack: j'ai le corrigé et la solution particulière de l'équa diff qui est:
y(t)=(e^-t)*[t/8*cos(2t)+t²/4*sin(2t)], donc le-1/32 est donc en trop
Je souhaite toujours résoudre cette équa diff par la méthode des transformées de Laplace et je serai reconnaissant à toute contribution qui me permette de conclure...
Cordialement lefouineur
@mathelot: décomposer une fraction rationnelle en éléments simples, ma calculette sait le faire, et moi aussi.
@Pisigma: je pense aussi qu'il manque à mon équation en p les conditions initiales mais l'énoncé ne les donne pas.
@Black Jack: j'ai le corrigé et la solution particulière de l'équa diff qui est:
y(t)=(e^-t)*[t/8*cos(2t)+t²/4*sin(2t)], donc le-1/32 est donc en trop
Je souhaite toujours résoudre cette équa diff par la méthode des transformées de Laplace et je serai reconnaissant à toute contribution qui me permette de conclure...
Cordialement lefouineur
Re: Equa diff et transformée de Laplace
lefouineur a écrit:Bonsoir mathelot, Pisigma et Black Jack, et merci pour vos réponses rapides.
@mathelot: décomposer une fraction rationnelle en éléments simples, ma calculette sait le faire, et moi aussi.
@Pisigma: je pense aussi qu'il manque à mon équation en p les conditions initiales mais l'énoncé ne les donne pas.
@Black Jack: j'ai le corrigé et la solution particulière de l'équa diff qui est:
y(t)=(e^-t)*[t/8*cos(2t)+t²/4*sin(2t)], donc le-1/32 est donc en trop
Je souhaite toujours résoudre cette équa diff par la méthode des transformées de Laplace et je serai reconnaissant à toute contribution qui me permette de conclure...
Cordialement lefouineur
Bonjour,
Non le 1/32 n'est pas en trop ... mais on peut le supprimer.
Mes solutions sont : y = e^-t * (A.cos(2t) + B.sin(2t)) + e^(-t) * [(t²/4 - 1/32).sin(2t) + t/8 * cos(2t)]
Et en posant B - 1/32 = C (donc en modifiant la constante d'intégration, ce qui peut évidemment se faire), on arrive à :
y = e^-t * (A.cos(2t) + C.sin(2t)) + e^(-t) * [(t²/4 * sin(2t) + t/8 * cos(2t)]
avec A et C des constantes ... à déterminer avec les conditions initiales.
Modifié en dernier par Black Jack le 13 Mai 2022, 10:39, modifié 1 fois.
Re: Equa diff et transformée de Laplace
Bonjour
Comme d'habitude ma réponse au MP reste "bloquée"
il faut bien que je réponde ici
Je vous aurai aidé volontiers mais je suis débordé :
je ne peux pas suivre un sujet qui me demanderai de réviser
(la transformée de Laplace, c'est très loin pour moi. Sur un sujet précédent je n'ai répondu qu'à la décomposition en éléments simples).
Je suis sûr que d'autres membres du forum vont vous aider
Bon courage à tous
Comme d'habitude ma réponse au MP reste "bloquée"
il faut bien que je réponde ici
Je vous aurai aidé volontiers mais je suis débordé :
je ne peux pas suivre un sujet qui me demanderai de réviser
(la transformée de Laplace, c'est très loin pour moi. Sur un sujet précédent je n'ai répondu qu'à la décomposition en éléments simples).
Je suis sûr que d'autres membres du forum vont vous aider
Bon courage à tous
Re: Equa diff et transformée de Laplace
Rebonjour,
Pour utiliser Laplace, on a besoin des condition initiales
En prenant par exemple les conditions initiales y(0) = 0 et y'(0) = 0, je trouve :
f(t) = 2*t * e^(-t) * cos(2t)
L(p) = 2*(p²+2p-3)/(p²+2p+5)²
p².Y(p)+2p.Y(p)+5.Y(p) = 2*(p²+2p-3)/(p²+2p+5)²
Y(p) = 2*(p²+2p-3)/(p²+2p+5)³
Y(p) = 2/(p²+2p+5)² - 16/(p²+2p+5)³
y(t) = 2 * e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32
y(t) = 2 * e^(-t) * (-t/8.cos(2t) + (1/16).sin(2t)) + e^(-t) * (t²/8.sin(2t)+3t/16.cos(2t)-3/32.sin(2t))
y(t) = 2 * e^(-t) * [(-t/8 + 3t/16).cos(2t) + ((1/16) - (3/32) + (t²/8)).sin(2t)]
y(t) = (1/16) * e^(-t) * [2t.cos(2t) + (4t²-1).sin(2t)]
*****
On peut probablement laisser les conditions initiales en littéral pour trouver les solutions générales ... mais je n'ai pas essayé.

Pour utiliser Laplace, on a besoin des condition initiales
En prenant par exemple les conditions initiales y(0) = 0 et y'(0) = 0, je trouve :
f(t) = 2*t * e^(-t) * cos(2t)
L(p) = 2*(p²+2p-3)/(p²+2p+5)²
p².Y(p)+2p.Y(p)+5.Y(p) = 2*(p²+2p-3)/(p²+2p+5)²
Y(p) = 2*(p²+2p-3)/(p²+2p+5)³
Y(p) = 2/(p²+2p+5)² - 16/(p²+2p+5)³
y(t) = 2 * e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32
y(t) = 2 * e^(-t) * (-t/8.cos(2t) + (1/16).sin(2t)) + e^(-t) * (t²/8.sin(2t)+3t/16.cos(2t)-3/32.sin(2t))
y(t) = 2 * e^(-t) * [(-t/8 + 3t/16).cos(2t) + ((1/16) - (3/32) + (t²/8)).sin(2t)]
y(t) = (1/16) * e^(-t) * [2t.cos(2t) + (4t²-1).sin(2t)]
*****
On peut probablement laisser les conditions initiales en littéral pour trouver les solutions générales ... mais je n'ai pas essayé.
Re: Equa diff et transformée de Laplace
Bonjour Black Jack et merci beaucoup pour le mal que t'est donné.
Bonjour Rdvn et merci pour ta réponse rapide.
Cordialement lefouineur
Bonjour Rdvn et merci pour ta réponse rapide.
Cordialement lefouineur
Re: Equa diff et transformée de Laplace
Black Jack a écrit:
Y(p) = 2/(p²+2p+5)² - 16/(p²+2p+5)³
y(t) = 2 * e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32
Comment passe-t-on d'une ligne à la suivante ?
Re: Equa diff et transformée de Laplace
mathelot a écrit:Black Jack a écrit:
Y(p) = 2/(p²+2p+5)² - 16/(p²+2p+5)³
y(t) = 2 * e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32
Comment passe-t-on d'une ligne à la suivante ?
Ou bien on est matheux et on a le courage de le faire ... et ce n'est pas mon cas.
Ou bien on n'est pas matheux et on confie le calcul à un logiciel ad hoc, par exemple ici :
https://www.emathhelp.net/fr/calculator ... alculator/
Re: Equa diff et transformée de Laplace
je pense qu'il y a une petite coquille dans la transformée inverse de la 2ème fraction
le dénominateur c'est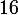 au lieu de
au lieu de 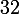
la transformée inverse de^2+2^2]^3}\, vaut\,y_2(t)= \dfrac{1}{8a^5}[(3-4\,t^2)sin(2\,t)-3.2t\, cos(2t)])
^2+2^2]^3} ,y_2(t)= \dfrac{-1}{16}[(3-4t^2)sin(2\,t)-3.2 t\, cos(2t)])
ou
= \dfrac{1}{16}[(4t^2-3)sin(2\,t)+6 t\, cos(2t)])
sauf erreur de recopie!
le dénominateur c'est
la transformée inverse de
ou
sauf erreur de recopie!
Re: Equa diff et transformée de Laplace
Pisigma a écrit:je pense qu'il y a une petite coquille dans la transformée inverse de la 2ème fraction
le dénominateur c'estau lieu de
la transformée inverse de
ou
sauf erreur de recopie!
Salut,
Erreur de recopie ... mais réponse finale correcte je pense.
Cette ligne ci : y(t) = 2 * e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32
aurait du être : y(t) = 2 * [e^(-t) * (-2t.cos(2t) + sin(2t))/16 + e^(-t) * (4t².sin(2t)+6t.cos(2t)-3.sin(2t))/32]
Je recommence :
Y(p) = 2/(p²+2p+5)² - 16/(p²+2p+5)³
y(t) = e^-t * (-2t.cos(2t) + sin(2t))/8 + e^-t * ((4t²-3).sin(2t) + 6t.cos(2t))/16
y(t) = e^-t * (-4t.cos(2t) + 2sin(2t))/16 + e^-t * ((4t²-3).sin(2t) + 6t.cos(2t))/16
y(t) = e^-t * [-4t.cos(2t) + 2sin(2t) + (4t²-3).sin(2t) + 6t.cos(2t)]/16
y(t) = (1/16) * e^-t * [2t.cos(2t) + (4t²-1).sin(2t)]
Re: Equa diff et transformée de Laplace
Black Jack a écrit:Pisigma a écrit:je pense qu'il y a une petite coquille dans la transformée inverse de la 2ème fraction
le dénominateur c'estau lieu de
Erreur de recopie ... mais réponse finale correcte je pense.
Je m'en doutais puisque ta réponse finale était correcte
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
