Ensembles

[MacManus]

Bonjour !

j'aurais besoin d'un peu d'aide sur les questions suivantes...

1/
soient F un ensemble infini non dénombrable et E (inclus dans F) un ensemble dénombrable. Montrer que F\E est infini non dénombrable.
2/
Montrer que Z,Q et NxN sont dénombrables.

Rq : par exemple je sais que R est infini non dénombrable. Si je prends E (inclus dans R) dénombrable, comment montrer que R\E (le complémentaire de E dans R) est infini non dénombrable ??

Merci à vous !

[Doraki]

Il faut définir une bijection entre F = E union (F\E) et F\E, pour en déduire qu'ils ont même cardinalité.

[MacManus]

d'accord merci Doraki.

soit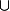 f : E (F\E)F\E définie par :

f(x) = g(x), si x E
f(x) = h(x), si x (F\E)

avec g : E(F\E) et h : (F\E)(F\E)

Il faut montrer en fait que f est bijective c'est bien ça ??!
est-ce qu'on peut dire ici que g est injective (Card(E)Card(F\E)) ??
Que dire de h...bijective ??
le problème c'est que (F\E) est infini non dénombrable, donc peut-on parler de cardinalité ??

merci pour votre aide !

[Maxmau]

Bonjour !

1/
soient F un ensemble infini non dénombrable et E (inclus dans F) un ensemble dénombrable. Montrer que F\E est infini non dénombrable.

Bj

Q1 - Si F\E est au plus dénombrable, E U (F\E ) = F n'est-il pas dénombrable ?

[Doraki]

d'accord merci Doraki.

soit f : E (F\E)F\E définie par :

f(x) = g(x), si x E
f(x) = h(x), si x (F\E)

D'où tu sors tes fonctions g et h ? tu comptes en parler sans avoir dit ce qu'elles faisaient ??
Si tu comptes donner une définition de f, faut que tu précises ce que sont g et h sinon ce que tu écris ne veut absolument rien dire.

Il faut pas montrer que f est bijective, il faut trouver g et h telles que la fonction f obtenue soit bijective.


Ou sinon tu fais un raisonement par l'absurde c'est vrai que c'est un peu plus simple à trouver

[mathelot]

Bjr,
voilà deux trois petites choses pour t'aider:

un entier naturel non nul s'écrit:

en factorisant la plusgrande puissance de 2 qui le divise.

s'énumére, se parcourt ainsi:
0,1,-1,2, -2, 3,-3,4,-4,5,-5,..

il reste éventuellement à écrire la bijection de sur qui va avec cette énumération.

D'autre part, on peut associer ensuite


ce qui devrait permettre de numéroter les fractions positives..

écrire les 10 premieres !!

[MacManus]

Merci à vous pour vos réponses.
Donc si j'ai bien compris mathelot, tout entier naturel s'écrit comme le produit d'une puissance de 2 et d'un nombre impair. (p et k entiers naturels).
En fait on peut trouver plusieurs bijections de N sur Z (selon l'énumération de Z, c'est bien ça?).
Z = N U (-N) et la bijection associée est f(p)=-p (p entier naturel non nul).
Donc Z est dénombrable. de même pour Q d'après ton raisonnement.Pour NxN j'ai compris comment procéder.

en revanche pour la question 1 je reste toujours bloqué, je ne parviens pas à trouver de bijection....

merci

[Maxmau]

Bj

Il y a une grosse différence entre:
1/ Etablir l'existence d'une bijection
2/ Exhiber une bijection

[MacManus]

d'accord ici on serait plutôt dans le 1er cas...

[mathelot]

Merci à vous pour vos réponses.
Donc si j'ai bien compris mathelot, tout entier naturel s'écrit comme le produit d'une puissance de 2 et d'un nombre impair. (p et k entiers naturels).

vi. ça permet de numéroter quelques ensembles comme et .

En fait on peut trouver plusieurs bijections de N sur Z (selon l'énumération de Z, c'est bien ça?).

oui, on peut par exemple, composer à droite une telle bijection
par une permutation de

[Doraki]

Z = N U (-N) et la bijection associée est f(p)=-p (p entier naturel non nul).

J'ai pas compris.

[Maxmau]

en revanche pour la question 1 je reste toujours bloqué, je ne parviens pas à trouver de bijection....

merci

La première question ne demande pas d’établir que F et F\E sont équipotents mais simplement que F\E est infini non dénombrable. Je pense avoir donné le moyen de résoudre cette question dans mon premier message.

Cependant, Il est vrai que F et F\E sont équipotents. (voir résultats de cours sur les cardinaux)