Suite d'ensembles !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 16 Aoû 2007, 01:32
par legeniedesalpages » 16 Aoû 2007, 01:32
Salut Barbu

Tu peux montrer que

par l'absurde.
Supposons que

n'est pas inclus dans

. Cela revient à dire que
 \cap (E\setminus A) \neq \emptyset)
, c'est à dire il existe un point

de

qui est dans

et qui n'est pas dans

.
Rappel des définitions: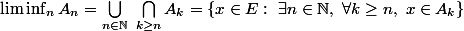
,
\Longleftrightarrow [(\forall x\in A,\ \exists n_0\in \mathbb{N}:\ n\geq n_0\ \Longrightarrow\ x\in A_n)\ \mbox{ et } (\forall x\notin A,\ \exists n_0\in \mathbb{N}:\ n\geq n_0\ \Longrightarrow\ x\notin A_n)])
.
Comme

, il existe un entier
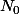
tel que
[CENTER]

.[/CENTER]
Comme
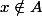
, il existe un entier
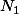
tel que
[CENTER]

.[/CENTER]
Donc pour tout
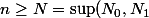)
, on a

et

, ce qui est absurde.
Donc
 \cap (E\setminus A) = \emptyset)
, autrement dit

.
Sauf erreur.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Aoû 2007, 01:43
par barbu23 » 16 Aoû 2007, 01:43
:++:
Jolie demonstration "legeniedesalpages" ...
Merci beaucoup !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Aoû 2007, 23:49
par barbu23 » 16 Aoû 2007, 23:49
Bonsoir :
J'espère que tu es là "legeniedesalpages" :
J'ai un truc à te demander :
Tu as defini, dans ton dernier message ,

par :

.
Est ce que tu peux faire la même chose avec :

... c'est à dire :

.
et merci infiniment !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Aoû 2007, 00:11
par barbu23 » 17 Aoû 2007, 00:11

.
C'est pourquoi tu as écrit :

Maintenant :

Donc voilà :

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Aoû 2007, 00:56
par barbu23 » 17 Aoû 2007, 00:56
Et si on veut maintenant montrer que :

.. comment faire ?!
Par absurde ?! ( Mais ça marche pas.. ! )
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Aoû 2007, 15:07
par barbu23 » 17 Aoû 2007, 15:07
:help: :help: :help: pls !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Aoû 2007, 17:46
par barbu23 » 17 Aoû 2007, 17:46
Je vais essayer de resoudre ça par absurde !
Supposons que :

.

 \bigcap A^{C} \neq \empty $)


:

et


:


:


Pour

,

:



:

et

( absurde ).
Par conséquent :

.
 par legeniedesalpages » 25 Aoû 2007, 13:37
par legeniedesalpages » 25 Aoû 2007, 13:37
salut barbu,
désolé je suis en italie depuis une dizaine de jours, et donc loin de mon pc.
Oui tu peux définir comme tu l'as fait

,
et ta démo tient la route pour montrer que

.
à+
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 25 Aoû 2007, 17:05
par barbu23 » 25 Aoû 2007, 17:05
D'accord "legeniedesalpages", merci !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités