Bonjour, je viens d'entrer en MPSI, et dans un exercice, on étudie l'ensemble
D = {zC, |z - 1/2| < 1/2} et f telle que z --> z (1-z).
J'essaye de montrer que D est stable par f, soit f(z) D, puis déterminer l'ensemble des images de points de f(D), et enfin trouver les z tels que f(z) = z, mais je ne vois pas comment commencer. J'ai essayé de bricoler les inéquations mais j'ai quelques problèmes avec la notion de "module" dans ce genre d'exercices, comment s'en débarasser, etc. Est-ce que je peux résoudre une inéquation "normale" ? Faut-il poser z = x+iy ? :triste:
Merci bien.
Ensembles complexes de points
9 messages
- Page 1 sur 1
re,
les nombres complexes h de module , constituent le disque ouvert H centré en l'origine, de rayon
, constituent le disque ouvert H centré en l'origine, de rayon 
Pour un h fixé, comment situe-t-on le point d'affixe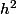 ? (avec la forme trigo)
? (avec la forme trigo)
répondre à cette question donne l'image de H par
l'application
si on considère ce "mouvement", on voit qu'il ne s'agit pas d'une rotation,
car dans le sens trigo, les points tournent de plus en plus rapidement
puisque=2Arg(h))
-------------------------------
Pour l'équation f(z)=z
 est un corps, les éléments non nuls y sont inversibles
est un corps, les éléments non nuls y sont inversibles
donc réguliers, on peut simplifier les deux membres de l'équation par z si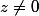
les nombres complexes h de module
Pour un h fixé, comment situe-t-on le point d'affixe
répondre à cette question donne l'image de H par
l'application
si on considère ce "mouvement", on voit qu'il ne s'agit pas d'une rotation,
car dans le sens trigo, les points tournent de plus en plus rapidement
puisque
-------------------------------
Pour l'équation f(z)=z
donc réguliers, on peut simplifier les deux membres de l'équation par z si
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
