Ensembles de points
10 messages
- Page 1 sur 1
Pour ce système j'ai trouvé que l'ensemble solution est un secteur angulaire ayant pour sommet le point d'intersection I(20/3;-4/3) des droites (d):y=-1/2x+2 et (d'):y=-2x+12 et ayant pour côtés d'une part la demi-droite, partie de (d) d'origine I et passant par O et d'autre part la demi-droite, partie de (d') d'origine I et passant par O. Je ne suis pas d'ailleurs très sûre de ce résultat...
Mais je ne vois pas comment réduire l'ensemble avec les deux premières conditions
Mais je ne vois pas comment réduire l'ensemble avec les deux premières conditions
salut
1/ évidemment il y a une infinité de solutions ...
quand on dit "déterminer" c'est plutôt le représenter dans le plan ....
ici l'ensemble des solutions est l'intersection de quatre demi-plans ...
puisque la relation ax + by + c ? 0 (où ? représente un quelconque symbole d'inégalité) est un demi-plan de frontière la droite d'équation ax + by + c = 0
2/
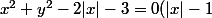^2 + y^2 = 4)
....
1/ évidemment il y a une infinité de solutions ...
quand on dit "déterminer" c'est plutôt le représenter dans le plan ....
ici l'ensemble des solutions est l'intersection de quatre demi-plans ...
puisque la relation ax + by + c ? 0 (où ? représente un quelconque symbole d'inégalité) est un demi-plan de frontière la droite d'équation ax + by + c = 0
2/
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
1/ évidemment il y a une infinité de solutions ...
quand on dit "déterminer" c'est plutôt le représenter dans le plan ....
ici l'ensemble des solutions est l'intersection de quatre demi-plans ...
puisque la relation ax + by + c ? 0 (où ? représente un quelconque symbole d'inégalité) est un demi-plan de frontière la droite d'équation ax + by + c = 0
2/
....
Pour la 2), il y a aussi moyen de distinguer le cas x>=0 et x<=0
On voit que chacun de ces cas amène à un arc de cercle bien défini
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
