Ensembles et applications

[Anonyme]

bonjour, je n'arrive pas à faire cet exercice, j'ai compris le cours mais je n'arrive pas à commencer l'exercice, je ne vois pas quelle est la méthode à utiliser:

1. Soit f une injection de N dans N telle que pour tout n> ou égal à 0, f(n) ou égal à n.
2. Soit f une bijection de N dans N. Montrer que pour tout M> ou égal à 0, il existe N tel que n>ou égal à N => f(n)>ou égal à M. Cette propriété revient à dire que la limite f(n) lorsque n tend vers l'infini est n. Cette propriété est-elle vérifiée pour une injection? Une surjection?

J'espère que vous aurez du temps pour m'aider à comprendre la méthode. Je vous remercie.

[Alpha]

Salut, c'est un problème sympathique, mais pas très difficile. En fait, l'idée est de procéder par récurrence.

Déjà, , mais puisque est une application de dans . Donc .

Ensuite, tu supposes que pour tout entre et inclus, .

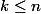
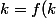Alors on a bien sûr , mais d'autre part, comme est une injection, et que pour tout , , on a différent de . Donc

et d'autre part . Donc

Donc .

Et voilà, le tour est joué. Même idée, je pense, pour la suite.

Codialement :happy3:

[Anonyme]

merci pour votre réponse.
par contre je n'ai pas bien compris l'étape f(n+1) différent de f(k). apparemment c'est par rapport à l'injection, qu'est-ce qui est utilisé?
pour la deuxieme partie de la question quand f est une surjection, au début la démonstration est la même, mais qu'est ce que je dois utiliser par rapport à la surjection pour arriver à la conclusion?

[Galt]

Dans une injection, deux éléments distincts ne peuvent pas avoir la même image. Comme on a f(0)=0, f(1)=1....f(n)=n par hypothèse de récurrence, f(n+1) ne peut pas être égal à0, ni à 1, ni... ni à n puisque ces images ont déjà été obtenues.

[Anonyme]

merci!!!!!!!!!!!
pour la surjection par contre c'est possible que 2 éléments distincts aient la même image, non? ou alors je n'ai rien compris. mais après je ne vois pas comment terminer la démo.

[khivapia]

oui c'est possible pour une surjection que deux éléments aient la même image... Ce n'est que pour l'injection que ce n'est pas possible.

Bonne soirée

[Anonyme]

ça y est j'ai fait celui sur la surjection. :)
désolée d'en rajouter encore une couche, maus je veux être sûre de bien comprendre: quel est le raisonnement qui permet de passer de l'étape nencore merci!

[Alpha]

Bonsoir, Gwenn,

si , tu peux tout de suite en déduire que , par définition de en quelque sorte.

En effet, dans, signifie.

Par conséquent on a , ce qui implique .

Si tu as d'autres questions, n'hésite pas.

Cordialement :happy3:

Apha +

PS : Inscris-toi si tu veux, ça ne coût rien!

[Anonyme]

ok pour la premiere question, tout est clair, c'est génial. pour la deuxieme question, j'ai essayé de raisonner plus ou moins de la même manière: initialisation sur M=0, hérédité avec M>0, je suppose k dans N tel que f(k) f(k)...mais là je sais que je m'embrouille et c'est un peu la cata, en fait, je ne sais pas trop comment faire. est ce que le début est bon? si vous pouvez m'aider à trouver comment arriver à la conclusion, ça serait super! merci.