Ensemble infini

[mehdi-128]

Bonjour,

L'exercice était de déterminer une application injective mais non surjective. On a :



Puis déterminer une application surjective mais non injective.



Mais je ne comprends pas la remarque suivante : chacun des 2 exemples suivants prouve que n'est pas fini.

Ma définition d'ensemble fini est :

L'ensemble est fini s'il existe et une bijection de sur .

Mais quel rapport avec l'exercice ?

Ou bien est-ce le résultat de l'exercice suivant ?

Soit un ensemble. Si contient une suite d'éléments 2 à 2 distincts alors est infini.

[pascal16]

perso, tenter de démontrer une propriété à partir de cette propriété ne constitue pas une preuve.
Il y a peut-être un point qui le démontre dans la construction du cours que tu suis.

pour moi, l'infinité de N est axiomatique et ne peux être démontrée avec des éléments de N.
Ton dernier résultat est lui pertinent, c'est la base de l'infini dénombrable.

[mehdi-128]

Ok merci.

Soit un ensemble.

Si contient un ensemble infini, alors il est infini.
C'est simplement la contraposée de : "Si est un sous ensemble de avec fini alors est fini."

Soit une suite d'éléments de 2 à deux distincts. Alors l'application est injective et donc induit une bijection de sur son image qui est alors une partie infinie de car . Par suite, est infini.

[infernaleur]

Si N était finit on aurait comme l’application est injective elle serait aussi surjective

[mehdi-128]

Si N était finit on aurait comme l’application est injective elle serait aussi surjective

Je n'ai pas compris. De quelle application parlez vous ?

[beagle]

Si N était finit on aurait comme l’application est injective elle serait aussi surjective

Je n'ai pas compris. De quelle application parlez vous ?

Bah de la tienne en premiere ligne du premier message.

E et F sont finis et j'ai une injection pas surjective,
alors cardinal de F c'est E les elements de F qui ont un ATCD, PLUS les éléments permettant non surjection = les éléments de F sans ATCD.
F plus grand que E

idem avec surjection non injective,
cardinal de E maintenant est celui de F un élément de F ayant son ATCD , PLUS les éléments de F ayant deux ou plus ATCD(moins 1 certes)
E plus grand que F

C'est très cousin des ensembles meme infini par double injection ou double surjection….

PS: j'ai fait avec le cardinal, on peut faire idem avec de l'inclusion stricte.
un ensemble fini qui un cardinal supérieur à son cardinal cela n'existe pas.
un ensemble fini strictement inclue dans lui-même cela n'existe pas non plus

[GaBuZoMeu]

Une définition classique d'ensemble infini est : un ensemble est infini s'il existe une bijection de sur un sous ensemble strict .
La fonction successeur donne une telle bijection.

Il n'est pas tout à fait évident de démontrer que, pour tout ensemble qui n'est pas infini au sens de la définition précédente, il existe un entier naturel et une bijection de sur l'ensemble des entiers naturels .

[lyceen95]

Ma définition d'ensemble fini est :

L'ensemble est fini s'il existe et une bijection de sur .

Cette définition n'est ni vraie, ni fausse, elle ne veut rien dire.

[beagle]

Est ce qu'un ensemble qui ne serait pas fini pourrait ne pas ètre infini?
= si on montre que pas fini est-il infini,

ou existe-t-il des ensembles non finis, non infinis, des ensembles à terminer par exemple?

[GaBuZoMeu]

Cette définition n'est ni vraie, ni fausse, elle ne veut rien dire.

Parler de vérité ou de fausseté d'une définition n'a pas de sens. Et cette définition veut dire quelque chose : elle veut dire exactement ce qu'elle dit.

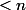
Soit un ensemble tel qu'il existe un entier naturel et une bijection de sur l'ensemble des entiers naturels . Alors il n'existe pas de bijection de sur une partie stricte de lui-même. La démonstration peut se faire par récurrence sur .

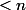
Soit un ensemble tel qu'il n'existe aucune entier naturel tel qu'il existe une bijection de sur l'ensemble des entiers naturels . Alors on peut construire par récurrence une injection de dans (en utilisant l'axiome du choix dépendant, une forme faible d'axiome du choix - voir wikipedia - qui me semble nécessaire ici). Partant de là on peut facilement construire une bijection de sur une partie stricte de lui-même.

[lyceen95]

Ok, ce qui peut se reformuler en :

L'ensemble E est fini s'il existe n appartenant à N et une bijection de [1,n] sur E.

Ce qui est un petit peu différent de la définition précédente. Dans la définition précédente on définissait un ensemble fini qui était forcément N.