- Ton

, ça risque pas d'être un corps vu que déjà Z ça en est pas un : par exemple tu peut me dire qui c'est l'inverse de

?
- Ensuite, là où tu "mélange un peu tout", c'est que pour pouvoir
démontrer que toute les solutions s'obtiennent à partir d'une "solution minimale", 'il faut bien évidement avoir une définition
on ne peut plus propre de ce qu'on entend par
minimale et que là, ça ne semble pas très clair dans ta tête :
Si on prend par exemple d=5 alors x=51841 ; y=-23184 est effectivement une solution dans Z² qui en terme de "distance du point (x,y) au point (0,0)" est effectivement "très très grande" alors qu'avec l'autre relation dot tu parlait consistant à regarder la valeur du nombre réel

elle est très très petite :

. Et c'est pour ça que je te disait que les deux notion de "petit" ne coïncidaient pas et que la deuxième vision (avec des réels) n'était pas la bonne.
Donc si on veut avoir des chance que ça fonctionne, parmi les différentes possibilités que tu as évoqué, un trux qui peut marche pour "comparer" des solutions, c'est effectivement de regarder la distance des points (x,y) et (x',y') à l'origine, c'est à dire de décréter que,
par définition, on dira que la solution (x,y) est "plus petite" que la solution (x',y') lorsque

c'est à dire

.
Et c'est évidement infiniment plus malin du fait en particulier que, si x et y sont dans Z alors x²+y² est dans N et que toute partie non vide de N admet un plus petit élément donc pour montrer qu'il y a une "solution minimale" y'aura juste à montrer qu'il y a au moins une solution.
Par contre, il faut faire gaffe au fait que dans ce cas les "solutions minimales", c'est bien évidement
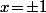
;

donc ta soluce
)
il faut bien sûr dire qu'elle est minimale
parmi les solutions autres que )
.
Une fois que ça c'est bien clair, c'est à dire qu'on a bien dégagé ce que l'on entendait par "plus petite" et par "solution minimale", à ce moment là (et pas avant), on peut se lancer dans des calculs et ce qu'il faut faire, c'est montrer que, partant d'une solution (x,y) quelconque (ou presque...) on peut construire une solution (x',y') "plus petite",
c'est à dire telle que x'²+y'²<x²+y².
Et effectivement, le (x',y') en question, on l'obtient par division en faisant

(où
)
est ta "solution minimale") mais surement pas en faisant comme tu le fait la division de n'importe quelle solution par n'importe quelle autre solution vu que :
- Je vois pas l'intérêt de piocher
deux solutions quelconques vu la question posée : "
toute solution (x,y) est de la forme ...."- Je vois aucune raison particulière pour que la nouvelle solution obtenue soit "plus petite" que (x,y)
- Je vois pas comment tu fera ensuite le lien avec la question posée qui parle de "solution minimale" si dans ta preuve tu n'utilise pas aussi cette fameuse "solution minimale".
Bref, et en résumé, ce qu'il faut que tu montre, c'est que "presque tout le temps", si on prend une solution (x,y) puis
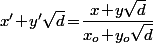
alors on aura

.

