Ensemble des bijections de N dans N
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 01 Oct 2010, 21:10
par Anonyme » 01 Oct 2010, 21:10
Bonsoir, je voudrais savoir si l'ensemble des bijections de N dans N est équipotent à N ou à R ? Merci d'avance :)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Oct 2010, 21:28
par girdav » 01 Oct 2010, 21:28
Bonjour,
cet ensemble a la même cardinalité que

.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Oct 2010, 21:46
par girdav » 01 Oct 2010, 21:46
Bon, je suppose que tu n'es pas intéressé que par la réponse mais aussi par une démonstration. On note
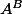
l'ensemble des applications de

dans

et

la cardinalité d'un ensemble

.
On peut montrer que
^{\mathbb{N}}|=|\{0,1\}^{\mathbb{N}^2}|)
. Si tu connais le résultat selon lequel

alors tu vois que l'on a
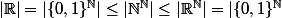^{\mathbb{N}}| =|\{0,1\}^{\mathbb{N}^2}|=|\{0,1\}^{\mathbb{N}}|=|\mathbb{R}|)
.
-
Anonyme
 par Anonyme » 01 Oct 2010, 21:56
par Anonyme » 01 Oct 2010, 21:56
Mais N^N, ce sont juste les applications non, pas les bijections ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Oct 2010, 22:01
par girdav » 01 Oct 2010, 22:01
Exact, j'ai lu un peu vite le premier post.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Oct 2010, 22:12
par girdav » 01 Oct 2010, 22:12
Je crois que je peux me rattraper en considérant l'application qui à une bijection de

dans

associe l'ensemble de ses points fixes. Cette application est une surjection de l'ensemble des bijections de

dans

dans l'ensemble des parties de

.
-
Anonyme
 par Anonyme » 01 Oct 2010, 22:31
par Anonyme » 01 Oct 2010, 22:31
Merci beaucoup !
-
Anonyme
 par Anonyme » 03 Oct 2010, 14:15
par Anonyme » 03 Oct 2010, 14:15
Et une bijection (pas continue) entre [a,b] et ]a,b[ ?
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 03 Oct 2010, 16:23
par euler21 » 03 Oct 2010, 16:23
Bonjour
pour construire une telle bijection je pense qu'il faut procéder ainsi:
on pose
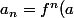 et b_n = f^{n}(b))
et pour tout n on doit avoir les deux familles d'éléments distincts deux à deux...
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 03 Oct 2010, 16:30
par euler21 » 03 Oct 2010, 16:30
Les suites

construits de façon à ce qu'elle soient d'éléments distincts, convergent toutes les deux vers deux valeurs
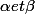
différentes. Après on pose
=\beta et f(\beta)=(\alpha))
et les autres éléments de [a,b] ont pour image eux-mêmes.
Je pense que ça peut faire l'affaire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Oct 2010, 16:33
par Ben314 » 03 Oct 2010, 16:33
euler21 a écrit:Bonjour
pour construire une telle bijection je pense qu'il faut procéder ainsi:
on pose
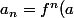 et b_n = f^{n}(b))
et pour tout n on doit avoir les deux familles d'éléments distincts deux à deux...
Si tu cherche des bijections "simples" (i.e pas forcément continues ou croissante ou...) de ]a,b[ dans [a,b] alors seul le cardinal de ]a,b[ et de [a,b] influe sur le résultat.
Si aR.
Ce nombre est clairement majoré par le nombre de fonctions de R->R qui est R^R=2^R et, en associant à toute partie A de R*+ la bijection f:R->R qui à x associe x si x est dans (Au-A) et -x sinon, on voit que le nombre de bijection de R->R est minoré par le nombre de parties de R*+ qui est égal à 2^R.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 03 Oct 2010, 16:41
par euler21 » 03 Oct 2010, 16:41
aarnaud a écrit:Et une bijection (pas continue) entre [a,b] et ]a,b[ ?
Salut Ben
Tout ce que j'ai essayé de faire c'est d'essayer de construire une telle bijection.
On sait que tous les intervalles (qui contiennent au moins deux éléments) ont le même cardinal que R.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
et pour tout n on doit avoir les deux familles d'éléments distincts deux à deux...
