Analyse bijections, dérivabilité, continuité

[Françoisdesantilles]

Bonjour à tous et bon week-end au passage

je poste ce message pour savoir si quelqu'un pouvais corrigé cet exercice svp?
Bonjour à tous et bon week-end au passage

https://zupimages.net/viewer.php?id=23/16/cs0u.jpeg

Je ne maitrise pas trop "les bijections", mais je ferai en sorte de répondre aux autres questions ici, le plus vite possible

[phyelec]

Bonjour,

1) Nombres qui appartiennent à Q ,exemples : ….-5/4, -4, -4.2, -3, -2, -1.524, -1/2, 0, +0.7, +1, +2, +2.41, +3, +4/5, +5, +6, +6.75, +7/2, +8…
Pour tous ces nombres , donc , et

2) Nombres qui appartiennent à R/Q ,exemples :,....
Pour tous ces nombres f(x)=0, donc ,

Votre réponse au 1a) vous ne traitez que la continué de f sur les points qui appartiennent à Q,quand est-il des points qui appartiennent à R/Q?
même remarque pour la question 2b)
pour la question 3) dites moi, 0 appartient à Q ou R/Q?

[Françoisdesantilles]

Bonjour,

1) Nombres qui appartiennent à Q ,exemples : ….-5/4, -4, -4.2, -3, -2, -1.524, -1/2, 0, +0.7, +1, +2, +2.41, +3, +4/5, +5, +6, +6.75, +7/2, +8…
Pour tous ces nombres , donc , et

2) Nombres qui appartiennent à R/Q ,exemples :,....
Pour tous ces nombres f(x)=0, donc ,

Votre réponse au 1a) vous ne traitez que la continué de f sur les points qui appartiennent à Q,quand est-il des points qui appartiennent à R/Q?
même remarque pour la question 2b)
pour la question 3) dites moi, 0 appartient à Q ou R/Q?

Bonjour, je ne voyais pas bien à quoi correspondait cet ensemble R privé de Q, c'est l'ensemble R sans les Quotient en fait?

[catamat]

Bonjour
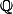\ est l'ensemble des irrationnels
Pour la continuité, peut on vraiment tracer un morceau de courbe sans lever le crayon ?

Ici il faut utiliser le fait que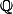 est dense dans
c'est à dire que tout intervalle ouvert dans contient des rationnels

de même \ 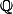est dense dans
c'est à dire que tout intervalle ouvert dans contient des irrationnels