Ensemble compact
15 messages
- Page 1 sur 1
ensemble compact
bonjour a tous,
j'aimerai savoir si mon raisonnement pour cette exo est juste : http://www.zupimages.net/viewer.php?id=19/24/j7qo.png
pour montré qu'il est fermé on prend une suite (xn,yn) de limite (x,y) appartenant à B, à la limite on obtient pour l'expression de gauche x²+x-6 <= 0 de plus "y" appartient à [0,1] et donc min{y , 1-y} appartient à [0,1/2] donc si x²+x-6 = 0 on à une absurdité car les solution sont -3 et 2 et donc on à que 4 ou 9 appartient à [0,1/2]
donc x²+x-6 < 0 donc (x,y) appartient à B et donc B est fermé
pour le faite qu'il soit borné on vois que B est inclus dans ]-3,2[ x [0,1] donc il est borné
j'aimerai savoir si mon raisonnement pour cette exo est juste : http://www.zupimages.net/viewer.php?id=19/24/j7qo.png
pour montré qu'il est fermé on prend une suite (xn,yn) de limite (x,y) appartenant à B, à la limite on obtient pour l'expression de gauche x²+x-6 <= 0 de plus "y" appartient à [0,1] et donc min{y , 1-y} appartient à [0,1/2] donc si x²+x-6 = 0 on à une absurdité car les solution sont -3 et 2 et donc on à que 4 ou 9 appartient à [0,1/2]
donc x²+x-6 < 0 donc (x,y) appartient à B et donc B est fermé
pour le faite qu'il soit borné on vois que B est inclus dans ]-3,2[ x [0,1] donc il est borné
Re: ensemble compact
L'idée est correcte, mais c'est mal rédigé.
Il faut mieux justifier pourquoi les éléments) de
de  vérifient
vérifient 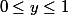 (et donc
(et donc 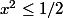 ). À ce moment-là on s'aperçoit que la première inégalité
). À ce moment-là on s'aperçoit que la première inégalité 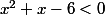 est superflue dans la description de
est superflue dans la description de  .
.
Il faut mieux justifier pourquoi les éléments
Re: ensemble compact
Faut être sérieux, "C'est mal rédigé" est un euphémisme.
Si tu as une idée pour montrer que B est fermé, il faut surtout reprendre le tout en essayant de formuler tes idées de façon plus claire.
Si tu as une idée pour montrer que B est fermé, il faut surtout reprendre le tout en essayant de formuler tes idées de façon plus claire.
Re: ensemble compact
Non, je maintiens que le raisonnement de Obito est correct, mais insuffisamment justifié ("y" appartient à [0,1]) et maladroit.
Il ne faut donc pas tout reprendre à zéro, mais il faut améliorer.
Il ne faut donc pas tout reprendre à zéro, mais il faut améliorer.
Re: ensemble compact
Moi par contre je ne comprends pas pourquoi tu es aussi agressif (envers moi et envers Obito31). Enfin pas grave, je pense qu'Obito31 pourra se débrouiller.
Re: ensemble compact
Bonjour merci pour ta réponse
Oui oui je sais^^ j'ai écrit ce post a l'arrache je voulais juste savoir si mon raisonnement était juste en fait
Mais donc d'après aviateur c'est faux ?
Oui oui je sais^^ j'ai écrit ce post a l'arrache je voulais juste savoir si mon raisonnement était juste en fait
Mais donc d'après aviateur c'est faux ?
Re: ensemble compact
Je pense qu'aviateur n'a pas compris ce que tu écrivais ("Les 3 premières lignes n'ont aucun sens"). Il faut dire que tu ne nous facilite pas la tâche. Essaie d'être un peu plus explicite et ordonne mieux tes arguments.
Re: ensemble compact
Obito31 a écrit:Bonjour merci pour ta réponse
Oui oui je sais^^ j'ai écrit ce post a l'arrache je voulais juste savoir si mon raisonnement était juste en fait
Mais donc d'après aviateur c'est faux ?
Non pas du tout; pour être plus précis, je dis simplement qu'arrivé à la 3ème ligne je n'ai rien compris.
Alors je ne peut pas dire que c'est bon ou faux. Et quand j'ai dit qu'il faut reprendre à zéro, et bien ça veut simplement dire "essayes de te faire comprendre" pour qu'on (je) puisse voir un raisonnement et là pouvoir dire "et bien oui c'est bon ou pas". C'est aussi simple que cela.
Re: ensemble compact
bonjour aviateur
j’espère être plus précis
considérons la 1er inégalité :
x²+x-6 < 0 <==> (x+3)(x-2) = 0 <==> x appartient ] -3 , 2 [
la 2eme :
x²<= min{ y, 1-y} ==> y >= 0 et 1-y >= 0 ==> y appartient à [0 , 1 ] de plus si y >= 1/2 alors 1-y <= 1/2
donc x² <= min{ y , 1-y } ==> x² appartient [ 0 , 1/2 ] ==> x appartient [ - rac(2)/2 , rac(2)/2 ]
maintenant si on prend une suite (Xn , Yn) appartenant à B de limite (X , Y) on a que Xn²+Xn-6 < 0 et Xn² <= min{ Yn , 1-Yn } et donc la limite vérifie X²+X-6 <= 0 et X² <= min { Y , 1-Y }
maintenant si X²+X-6 = 0 on à que X² est égale à 4 ou 9 ce qui absurde donc X²+X-6 < 0 et donc la limite appartient à B
et pour le caractère borné on vois que B est inclus dans [ -rac(2)/2 , rac(2)/2 ] x [ 0 , 1 ] donc B est borné
j’espère être plus précis
considérons la 1er inégalité :
x²+x-6 < 0 <==> (x+3)(x-2) = 0 <==> x appartient ] -3 , 2 [
la 2eme :
x²<= min{ y, 1-y} ==> y >= 0 et 1-y >= 0 ==> y appartient à [0 , 1 ] de plus si y >= 1/2 alors 1-y <= 1/2
donc x² <= min{ y , 1-y } ==> x² appartient [ 0 , 1/2 ] ==> x appartient [ - rac(2)/2 , rac(2)/2 ]
maintenant si on prend une suite (Xn , Yn) appartenant à B de limite (X , Y) on a que Xn²+Xn-6 < 0 et Xn² <= min{ Yn , 1-Yn } et donc la limite vérifie X²+X-6 <= 0 et X² <= min { Y , 1-Y }
maintenant si X²+X-6 = 0 on à que X² est égale à 4 ou 9 ce qui absurde donc X²+X-6 < 0 et donc la limite appartient à B
et pour le caractère borné on vois que B est inclus dans [ -rac(2)/2 , rac(2)/2 ] x [ 0 , 1 ] donc B est borné
Re: ensemble compact
Tu fais du travail un peu inutile.
En travaillant sur la deuxième inégalité (large), tu vois que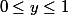 et que
et que 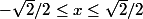 . Ceci montre déjà que
. Ceci montre déjà que  est borné. Par ailleurs tout
est borné. Par ailleurs tout ) qui vérifie la seconde inégalité vérifie la première. Cette première ne sert à rien, on peut l'oublier dans la description de
qui vérifie la seconde inégalité vérifie la première. Cette première ne sert à rien, on peut l'oublier dans la description de  . Cette deuxième inégalité revient à dire que la fonction continue
. Cette deuxième inégalité revient à dire que la fonction continue ) est négative ou nulle, donc
est négative ou nulle, donc  est fermé.
est fermé.
En travaillant sur la deuxième inégalité (large), tu vois que
Re: ensemble compact
Parce que l'image réciproque d'un fermé par une fonction continue est fermé. Ou si tu préfères, par passage à la limite dans les inégalités larges.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
