Endo qui commute avec toute isométrie => homothétie

[Matthieu31]

Bonsoir,

Je bloque sur un petit exercice d'algèbre linéaire...

Soit E un espace-vectoriel de dimension n finie, u un endomorphisme de E.
Montrer que si u commute avec toute isométrie vectorielle alors u est une homothétie.

Si quelqu'un à des pistes pour la dimension n quelconque... je bloque un peu :hein:

Merci d'avance !

[yos]

Une idée : essaie avec des isométries diagonalisables genre symétrie par rapport à un hyperplan. Et regarde u(F) pour F sep de l'isométrie.

[Matthieu31]

Très bonne idée, merci beaucoup j'ai pu finir l'exercice ainsi :happy2:

(Je ne sais pas si je suis censé expliciter le détail de la méthode pour d'autres usagers du forum ? Si oui merci de me faire signe et je résumerais ma démarche !)

Bonne soirée !

[yos]

Moi ça m'intéresse : tu as fait ça matriciellement?

[Matthieu31]

Considérons la symétrie orthogonale par rapport à l'hyperplan de vecteur normal le vecteur canonique de base 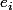avec compris entre et :

On a:



d'ou :

donc

d'ou pour tout il existe 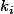dans K tel que :


Reprendre un raisonnement analogue avec la symétrie par rapport à l'hyperplan de vecteur normal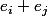 pour montrer que:


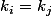
Voila, si j'ai réussi à faire une erreur la dedans merci de me le signaler

[yos]

Je vois deux problèmes :
L'espace propre associé à la valeur propre 1 est H et pas son orthogonal.
de plus il faut prouver que le coef est indépendant de i;

[Matthieu31]

Exact pour le 1 qui devrait être un -1, mais cela ne change strictement rien à la méthode, ce sera maintenant:

donc la conclusion reste la même.

Pour la fin c'est juste que je n'ai pas redétaillé:
Je prouve que tout les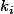 sont égaux en reconsidérant d'autres symétries, celles par rapport aux plans de vecteurs normaux e1+e2, puis e2+e3, etc... au final on trouve:
k1=k2=..=kn

[yos]

Oui ça roule je pense.
On peut aussi écrire que la matrice de u commute avec diag(-1,1,1,...,1) et d'autre du même genre. Mais c'est pas mieux.