Toute matrce compgne est la mat d'un endo cyclq

[Don vito]

S'il vous plait j'ai du mal à montrer la deuxième question , j'ai pensé à exprimer une matrice (des operations elementaires) et j'obtiens bien donc l'une comme le produit de l'autre fois une mat inversible mais ça n'a pas de rapport avec le caractère semblable.

[wserdx]

Considère x = le premier vecteur de la base canonique.

[Don vito]

(1)Je n'arrive pas à débloquer la situation, et puis une question( assez banale mais juste pour s'assurer) u^(n)(x)=x ?
(2)et puis quant à la question une, la matrice de u dans la base en question donne une matrice compagnon associé au polynome constant 1??
(3) quel sera le premier vecteur de la base canonique , E n'étant pas défini?

[wserdx]

Il me semble qu'une matrice compagne a des 1 sur la sous-diagonale, la dernière colonne contient les coefficients du polynôme, et des 0 partout ailleurs. Choisis 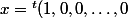(vecteur colonne = premier vecteur de la base canonique! )
Si est la matrice compagne, que vaut ?

On n'a jamais dit que mais simplement que est une combinaison linéaire de

[Don vito]

(1)oui en effet , mais ta remarque pour le x qui est premier vecteur de la base canonique , on l'obtient dans la dernière colonne de la matrice de l'endomorphisme cyclique exprimé dans la base citée.Donc sa matrice dans cette base est bien une matrice compagnon associée au polynôme constant 1.
Maintenant inversement, pour une matrice compagnon associée à un polynome P: je ne vois toujours pas comment faire.
(2)Sinon pour la valeur des puissances de U ma question était pour u cyclique, je suppose que c'est la même réponse n'est ce pas?

[wserdx]

Il me semble qu'une matrice compagne a des 1 sur la sous-diagonale, la dernière colonne contient les coefficients du polynôme, et des 0 partout ailleurs. Choisis (vecteur colonne = premier vecteur de la base canonique! )
Si est la matrice compagne, que vaut ?

On n'a jamais dit que mais simplement que est une combinaison linéaire de

Si est la matrice compagne, que vaut ?

u cyclique : ça ne veut pas dire que sa matrice est circulante : ne confonds pas!

[Don vito]

ok merci mais pourrais tu s'il te plait me donner une réponse à la question que j'ai noté (1) dans mon dernier poste;

[wserdx]

J'ai cru comprendre que tu disais : "Je ne vois pas comment faire".
Je te réponds par une nouvelle question:
Si est la matrice compagne, que vaut ?

[Don vito]

Je m'excuse ,je n'avais pas remarqué.
Ah oui c'est bon! Merci encore, enfait j'avais en tête mais bon j'ai pas fait attention à la définition de cyclique! :D

En effet: si on note la matrice compagnon Cp.et e1 =x. ek les autres elmts de la base.
Alors: Cp(e1)= e2
.
.
Cp(ep-1)=ep

or comme : (e1,...eP) est une base , alors (e1, ...,Cp(ep-1) ) est donc une base , d'ou la definition de cyclique.

Merci encore!!!!!!