Encadrement d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ariel60
- Membre Naturel
- Messages: 57
- Enregistré le: 09 Aoû 2016, 16:43
-
 par ariel60 » 25 Aoû 2016, 16:39
par ariel60 » 25 Aoû 2016, 16:39
Bonjour,
Avec cet exercice:
Soit x

R et on note E(x) la partie entière de x.On a
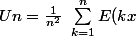=\frac{E(x)+E(2x)+...+E(nx)}{n^2})
Donner un encadrement simple de
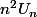
.
Là en partant de la définition de la partie entière,et en faisant la somme:
\leq x<E(x)+1)
\leq 2x<E(2x)+2)
\leq 3x<E(3x)+3)
...
\leq nx<E(nx)+n)
Je trouve que
}{2}<n^2 U_n + \frac{n(n+1)}{2})
Alors
n(n+1)}{2}<n^2U_n\leq \frac{x(n(n+1))}{2})
Ce qui contredit mon corrigé..mais où est l'erreur?D'après mon corrigé j'ai:
)}{2}-n<n^2U_n\leq \frac{x(n(n+1))}{2})
Merci d'avance.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 25 Aoû 2016, 18:12
par aymanemaysae » 25 Aoû 2016, 18:12
Bonjour,
Votre corrigé est juste car on a:
 \le x<E(x) + 1)
donc
 \le x<E(x) + 1 \le x+1)
donc
 \le x)
,
donc
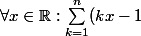 < \sum_{k=1}^n E(kx) \le \sum_{k=1}^n kx)
donc
}{2}x - n < n^2 U_n \le \frac{n(n+1) }{2}x)
,
l'erreur ou plutôt l'autre résultat, vient de l'application de la sommation à l'autre inégalité :
 \le x < E(x) + 1)
.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 25 Aoû 2016, 18:16
par Pseuda » 25 Aoû 2016, 18:16
ariel60 a écrit:Bonjour,
Avec cet exercice:
Soit x

R et on note E(x) la partie entière de x.On a
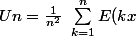=\frac{E(x)+E(2x)+...+E(nx)}{n^2})
Donner un encadrement simple de
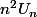
.
Là en partant de la définition de la partie entière,et en faisant la somme:
\leq x<E(x)+1)
\leq 2x<E(2x)+2)
\leq 3x<E(3x)+3)
...
\leq nx<E(nx)+n)
Je trouve que
}{2}<n^2 U_n + \frac{n(n+1)}{2})
Alors
n(n+1)}{2}<n^2U_n\leq \frac{x(n(n+1))}{2})
Ce qui contredit mon corrigé..mais où est l'erreur?D'après mon corrigé j'ai:
)}{2}-n<n^2U_n\leq \frac{x(n(n+1))}{2})
Merci d'avance.
Bonsoir,
Tu peux faire plus précis que ça :
\leq 2x<E(2x)+2)
,
Tu peux faire :
\leq 2x<E(2x)+1)
Tu peux aussi envisager l'encadrement différemment :
\leq 2x)
-
ariel60
- Membre Naturel
- Messages: 57
- Enregistré le: 09 Aoû 2016, 16:43
-
 par ariel60 » 25 Aoû 2016, 19:37
par ariel60 » 25 Aoû 2016, 19:37
aymanemaysae a écrit:l'erreur ou plutôt l'autre résultat, vient de l'application de la sommation à l'autre inégalité :
 \le x < E(x) + 1)
.
Je ne vois pas pourquoi je ne peux pas appliquer la somme à cette inégalité,puisque ceci conduit quand meme a la somme de E(kx).
Merci d'avance
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 25 Aoû 2016, 19:53
par aymanemaysae » 25 Aoû 2016, 19:53
Bonsoir,
à mon avis,
 \le x<E(x)+1)
permet d'encadrer les
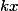
par les
)
alors
que l'autre inégalité permet l'inverse.
M. Pseuda , puisqu'il est là , est plus habilité que moi pour donner une réponse définitive.
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 25 Aoû 2016, 20:01
par danyL » 25 Aoû 2016, 20:01
aymanemaysae a écrit:M. Pseuda , puisqu'il est là , est plus habilité que moi pour donner une réponse définitive.
monsieur pseuda ou madame pseudo ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Aoû 2016, 10:10
par zygomatique » 26 Aoû 2016, 10:10
salut
ouais enfin ... si je peux me permettre : beaucoup de blabla pour pas grand chose :la simple définition de la partie entière et une élémentaire jonglerie sur l'inégalité de droite suffit :
 \le x < E(x) + 1 \\E(2x) \le 2x < E(2x) + 1 \\E(3x) \le 3x < E(3x) + 1 \\... \\E(nx) \le nx < E(nx) + 1)
en sommant ces n égalités :
 \le \dfrac 1 2 n(n + 1)x < \sum_1^n E(kx) + n)
donc immédiatement
x - n < \sum_1^n E(kx) \le \dfrac 1 2 n(n + 1)x) (*)
(*)...
ici l'erreur consiste à donner un encadrement qui ne permet pas d'utiliser le théorème des gendarmes : la différence entre les extrêmes ne tend pas vers 0
alors qu'avec
(*) et après avoir diviser par n² la différence des extrêmes tend vers 0

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
ariel60
- Membre Naturel
- Messages: 57
- Enregistré le: 09 Aoû 2016, 16:43
-
 par ariel60 » 26 Aoû 2016, 11:36
par ariel60 » 26 Aoû 2016, 11:36
alors finalement la suite tend vers (x/2).merci encore pour les reponses et les liens!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
R et on note E(x) la partie entière de x.On a
.
...
.