Suite,somme,encadrement

[singular]

Bonjour et heureuse fin d'année 2008, début d'année 2009, j'espère que vous pourrez me donner des indications concernant les questions sur lesquelles je bloque à propos de mes exos sur les suites, je vous les poserai sans doute au fur et à mesure:
Tout d'abord je bloque à cette question:
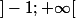
Montrer que pour tout x dans ,on a:

[fourize]

bonjour !

"bonne et heureuse année toi aussi"
concernant ta question, poser et
étudie sont tableau de variation.

ça te devait te suffir .

[singular]

merci Fourize.
Dans l'un de mes exos on pose
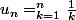
j'arrive sur l'encadrement suivant , afin de déterminer un équivalent de() en +l' infini, j'en déduis:
limlimlim 1+

J' imagine pouvoir en déduire que lim=1 ce qui me permettrait de dire que () est équivalent en + l'infini à ln(n), mais est ce que lim vaut bien 1 en + l'infini ?

[_-Gaara-_]

ln(n+1)/ln(n) ~ ln(n)/ln(n) = 1 ;)

[singular]

merci ....

[XENSECP]

Oui la suite harmonique est équivalente à ln(n) quoi

[singular]

A la fin de la première partie de cette exercice on a l'encadrement suivant: et on en déduit que en + est équivalent à ln(n)

Un peu plus loin dans l'exercice considérant cette même suite () tel que ,
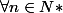
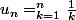
on pose la relation de récurrence =1 et
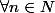
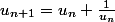
Après une petite série de question j'en ai déduis que cette suite est défini et strictement positif qu'elle est croissante strictement et divergente en +
J'ai conclu que ,

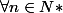
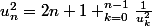
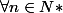
que et que la limite de (un) est donc +.

J'ai montré que

D'après ce qui m'est demandé par la suite je pense qu'il faille me servir de l'inégalité démontré plus haut: pour montrer que mais je n'y arrive pas, meci de me répondre.

[singular]

s'il vous plaît je ne veux pas laissé tomber :help:
Je fais d'autres exos bien sûre pour le momment.

[singular]

s'il vous plaît...

[singular]

c'est bon j'ai trouvé